EXAMPLES OF SOLVING TRIGONOMETRY WORD PROBLEMS

Example 1 :

A ramp for unloading a moving truck, has an angle of elevation of 30°. If the top of the ramp is 0.9 m above the ground level, then find the length of the ramp.

Solution :

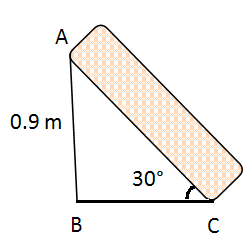
The side which is opposite to 90 degree is known as hypotenuse side, the side which is opposite to θ is known as opposite side and the remaining side is known as adjacent side.

In the given problem,we have to find the length of hypotenuse side and we know the length of opposite side.

AC = Hypotenuse side

AB = Opposite side

BC = Adjacent side

sin θ = opposite side/hypotenuse side

sin 30° = AB/AC

1/2 = 0.9/AC 

AC = 0.9 x 2 

AC = 1.8 m

Therefore, the length of ramp is 1.8 m.

Example 2 :

A girl of height 150 cm stands in front of a lamp-post and casts a shadow of length 150 √3 cm on the ground. Find the angle of elevation of the top of the lamp-post.

Solution :

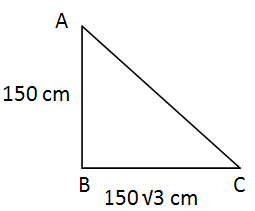
In the given problem,we have to find the angle inclined C.

AC = Hypotenuse side

AB = Opposite side = 150 cm

BC = Adjacent side = 150 √3 cm

tan θ = opposite side/Adjacent side

tan θ = AB/BC

tan θ = 150/150 √3

tan θ = 1/√3

θ = 30°

Example 3 :

Suppose two insects A and B can hear each other up to a range of 2 m. The insect A is on the ground 1 m away from a wall and sees her friend B on the wall, about to be eaten by a spider. If A sounds a warning to B and if the angle of elevation of B from A is 30°, will the spider have a meal or not ? ( Assume that B escapes if she hears A calling )

Solution :

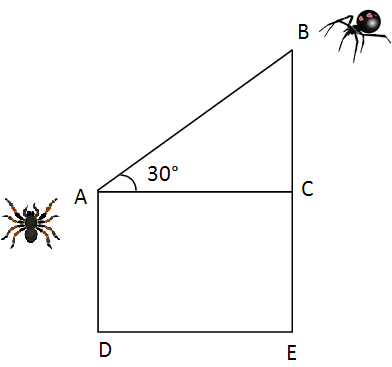
In the given problem,we have to the length of AB.

AC = Hypotenuse side

BC = Opposite side = 1 m

AC = Adjacent side

sin θ = Opposite side/Hypotenuse side

sin θ = BC/AB

sin 30° = 1/AC

1/2 = 1/AC

AC = 2 m

So, the spider B escapes.

Example 4 :

Evelyn Granville, who is 1.5 m tall, is standing 20 m from the base of a building. She sights the top of the building with an angle of elevation of 58°. Find the height of the building.

Solution :

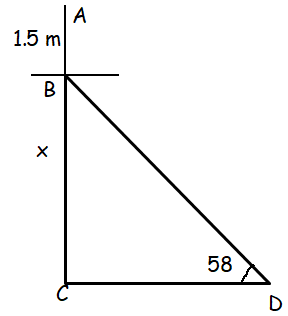
BC - height of the building

AB - height of the boy  1.5 m

CD - the distance between building and the point ==> 20 m

tan θ = Opposite side/adjacent side

tan 58 = BC/CD

1.6 = BC/20

BC = 20(1.6)

= 32 m

So, height of the building is 32 m.

Example 5 :

A video camera is mounted on the top of a 120 m tall building. When it tilts down 36° from the horizontal, it views the base of another building. When it tilts up 47° from the horizontal, it views the top of the same building.

a) How far apart are the two buildings?

b) How tall is the building viewed by the camera?

Solution :

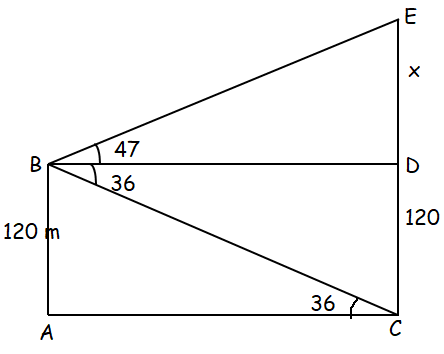
In triangle ABC,

tan θ = Opposite side/adjacent side

tan 36 = AB/AC

0.7265 = 120/AC

AC = 120/0.7265

AC = 165.17

Approximately 165 m

In triangle BDE,

tan 47 = DE/BD

BD = AC = 165

1.0723 = DE/165

DE = 1.0723 (165)

= 176.9

= 177 m

height of the building = 177 + 120

= 297 m

So, height of the building is 297 m.

Example 6 :

A wind swept tree grows at an angle of 85 degree. An environmental scientist wants to know the height of the tree. She walks 50 m from the base of the tree and measures an angle of elevation of 40 degree to the top of the tree. How tall is the tree?

Solution :

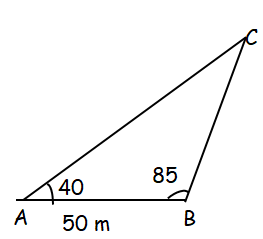
In triangle BDC, using sin law

a/sin A = b/sin B = c/sin C

BC = a, AB = c = 50 m, AC = b

C = 180 - (40 + 85)

C = 180 - 125

= 55

BC/sin 40 = AC/sin 85 = AB/sin 55

a/sin 40 = b/sin 85 = 50/sin 55

a/sin 40 = 50/sin 55

a = 50(sin 40) / sin 55

a = 50(0.642) / 0.819

= 32.1/0.819

= 39.19

= 39.2 m

So, height of the tree is 39.2 m

Example 7 :

The lighthouse L is 5 km from the nearest point P on the shore. T is the tree further down the shoreline such that PT is perpendicular to PL. If <PLT = 37 degree, determine the distance from P to T.

Solution :

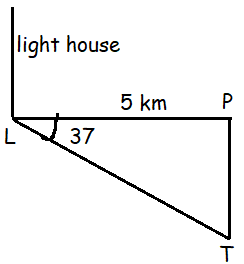
In triangle PLT,

tan θ = Opposite side/adjacent side

tan 37 = PT/PL

0.7535 = PT/5

PT = 5(0.7535)

PT = 3.7675

So, the distance from P to T is 3.77 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.