EXPECTED VALUE WORD PROBLEMS WITH SOLUTIONS

Problem 1 :

In a particular region in Africa, the probability that it will rain on any one day is 0.177. On how many days of the year would you expect it to rain?

Solution :

P(that it will rain)  =  0.177

P(number of days of year would we expect rain)

=  365(0.177)

=  64.61

So, approximately 65 days.

Problem 2 :

(a)  If 2 coins are tossed, what is the chance that they both fall heads?

(b)  If the 2 coins are tossed 300 times, on how many occasions would you expect them to both fall heads

Solution :

Possible outcomes  =  {HH, TT, HT, TH}

=  4

P(getting all heads)  =  1/4

Expected value when coins are tossed 300 times

=  300(1/4)

=  75 times.

When 2 coins are tossed 300 times, we can expect 75 times all heads.

Problem 3 :

A certain type of drawing pin, when tossed 400 times, landed on its back 144 times.

a) Estimate the probability that it will land on its back if it is tossed once.

(b)  If the drawing pin is tossed 72 times, how many “backs” would you expect?

Solution :

(a)  P(that it will land on its back)  =  144/400

=  0.36

Estimated probability is is 0.36.

Expected value when it is tossed 72 times  =  72(0.36)

=  25.92

So, we can expect back 26 times.

Problem 4 :

A bag contains 5 red and 3 blue discs. A disc is chosen at random and then replaced. This is repeated 200 times. How many times would you expect a red disc to be chosen?

Solution :

Total number of discs  =  5 red + 3 blue

=  8

P(Choosing red disc)  =  5/8

Expected value of choosing red disc, when it is repeated 200 times.

=  200(5/8)

=  125 times

Problem 5 :

A die has the numbers

0, 1, 2, 2, 3 and 4 on its faces.

The die is rolled 600 times. How many times might we expect a result of :

a)  0

b)  2

c)  1, 2 or 3

d) not a 4?

Solution :

Total possible outcomes  =  6

(a)  P(getting 0)  =  1/6

Expected result of 0 when the die is tossed 600 times :

=  600(1/6)

=  100

(b)  P(getting 2)  =  2/6

Expected result of 2 when the die is tossed 600 times :

=  600(2/6)

=  200

c)  P(Getting 1, 2 or 3)  =  4/6

Expected result of 1, 2 or 3 when the die is tossed 600 times :

=  600(4/6)

=  400

c)  P(not getting 4)  =  5/6

Expected result of not getting 4 when the die is tossed 600 times :

=  600(5/6)

=  500

Problem 6 :

A charity fundraiser gets a licence to run the following gambling game:

A die is rolled and the returns to the player are given in the ‘pay table’ alongside. To play the game $4 is needed. A result of ‘6’ wins $10, so in fact you are ahead by $6 if you get a ‘6’ on the first roll.

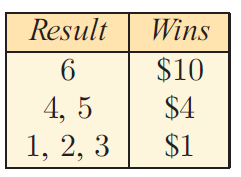
(a)  What are your chances of playing one game and winning:

i) $10   ii) $4   iii) $1 ?

(b) Your expected return from throwing a 6 is 1/6 x $10. What is your expected return from throwing :

(i) a 4 or 5   (ii) a 1, 2 or 3   (iii) a 1, 2, 3, 4, 5 or 6?

(c)  What is your expected result at the end of one game? Remember to include the cost of playing the game.

(d) What is your expected result at the end of 100 games?

Solution :

(a)  (i)  $10

To get $10, he has to get the result 6 on the die.

P(getting $10)  =  1/6

(ii)  P(getting $4)  =  2/6  ==>  1/3

(iii)  P(getting $1)  =  3/6  ==>  1/2

(b)  (i) a 4 or 5  =  (2/6) x 4  ==>  $1.33

(ii) a 1, 2 or 3  =  (1/2) x 1  ==>  $0.5

(iii) a 1, 2, 3, 4, 5 or 6  =  (1/6)(10) + (2/6) (4) + (3/6) (1)

=  (10/6) + (8/6) + (3/6)

=  (10+8+3)/6

=  21/6

=  $3.5

Problem 7 :

You draw one card from a standard deck of playing cards. If you pick a heart, you will win $10. If you pick a face card, which is not a heart, you win $8. If you pick any other card, you lose $6. Do you want to play? Explain

Solution :

Total number of cards n(S) = 52

Number of heart cards = 13

Face cards are 3 x 4 ==> 12

Face card excluding cards from heart

= 12 - 3

= 9

Other cards = 52 - 9 - 13

= 30

Probability of choosing heart card = 13/52

Probability of choosing face cards not from heart = 9/52

choosing other card = 43/52

Expected value

= (13/52) x 10 + (9/52) x 8 - (30/52) x 6

= 2.5 + 1.38 - 3.46

= 0.42

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.