EXPLORING PROPERTIES OF INTEGER EXPONENTS

Properties of integer exponents can be used to solve many real-world problems. 

So, it is always important to explore the properties of integer exponents. 

A. Look at the following equations and answer the questions given below. 

3 · 3 · 3 · 3 · 3 = 3⁵

(3 · 3 · 3 · 3) · 3 = 3⁴ · 3¹ = 3⁵

(3 · 3 · 3) · (3 · 3) = 3³ · 3² = 3⁵

1. What pattern do you see when multiplying two powers with the same base ?

The result has the same base with an exponent equal to the sum of the exponents in the powers.

2. Use your pattern to find the value of 'n' in the equation given below.

5²· 5³ = 5ⁿ -----(1)

We know the fact that the result has the same base with an exponent equal to the sum of the exponents in the powers. 

So, we have 

5²· 5³ = 5⁵ -----(2)

Comparing (1) and (2), we get n  =  5.

B. Look at the following equation and answer the question given below.  

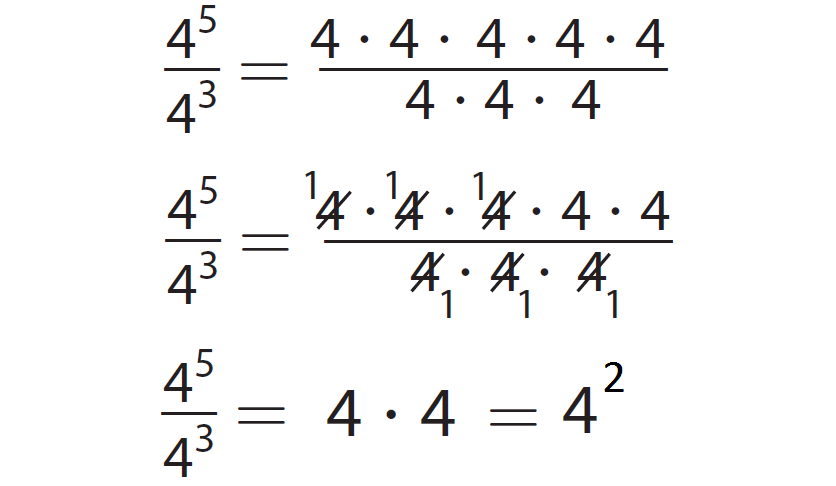
1. What pattern do you see when dividing two powers with the same base ?

The result has the same base with an exponent equal to the difference of the exponent in the numerator and exponent in the denominator.

2. Use your pattern to find the value of n in the equation given below.

6⁸/6³ = 6ⁿ -----(1)

We know the fact that the result has the same base with an exponent equal to the difference of the exponent in the numerator and exponent in the denominator.

So, we have 

6⁸/6³ = 6⁵-----(2)

Comparing (1) and (2), we get n  =  5.

C. Look at the following equation and answer the questions given below. 

(5³)² = 5³ · 5³

(5³)² = 5³⁺³

(5³)² = 5⁶

1. What pattern do you see when raising a power to a power ?

The result has the same base with an exponent equal to the product of the exponents.

2. Use your pattern to find the value of n in the equation given below.

(7²)⁵ = 7ⁿ -----(1)

We know the fact that the result has the same base with an exponent equal to the product of the exponents.

So, we have 

(7²)⁵ = 7¹⁰ -----(2)

Comparing (1) and (2), we get n = 10.

Reflect

1. General rule for the value of a^m ⋅ aⁿ.

a^m ⋅ aⁿ = a^{m + n}

2. General rule for the value of a^m ÷ aⁿ. a ≠ 0.

a^m ÷ aⁿ = a^{m - n}

3. General rule for the value of (a^m)ⁿ.

(a^m)ⁿ = a^mn

Problem 1 :

What do the expressions 3³ and 3⁴ have in common.

Solution :

• In 3³, we have three 3's
• In 3⁴, we have four 3's

In common, we have three 3's.

Problem 2 :

Write a multiplication expression without exponents that is equivalent to 3³.

Solution :

3³ means 3 should be repeated three times as product.

3³ = 3 x 3 x 3

Problem 3 :

Write a expression without exponents that is equivalent to 3³ ⋅ (3⁴) 

Solution :

3³ means 3 should be repeated three times as product.

3³ = 3 x 3 x 3

3⁴ means 3 should be repeated four times as product.

3⁴ = 3 x 3 x 3 x 3

3³ ⋅ (3⁴)  = 3 x 3 x 3 x 3 x 3 x 3 x 3

Problem 4 :

Explain why 5¹⁰/5² equal to 5⁸ 

Solution :

= 5¹⁰/5²

Since we have same bases on both numerator and denominator, using the properties of exponents, we have to put only one base and subtract the powers. So,

= 5^{10 - 2}

= 5⁸

Problem 5 :

Read the problem below. Then explore how to find the product of powers with the same base and same exponent.

(3²)⁴

Solution :

= (3²)⁴

Here the base = 3²

the power = 4

To keep the base and exponents as the same, we have to repeat the base 4 times as product.

3² x 3² x 3² x 3²

Problem 6 :

Simplify (3²)⁴

Solution :

 (3²)⁴

Since we have power raised by another power, we have to multiply the powers.

= 3^{2 x4}

= 3⁸

Problem 7 :

Simplify (2³)(4³)

Solution :

= (2³)(4³)

Since the bases are not same, to do the further simplification, we have to make the bases same.

4³ = (2²)³

Since we have a power raised by another power, we have to multiply the powers.

= 2⁶

Problem 8 :

Simplify (2¹⁸)²

Solution :

= (2¹⁸)²

Since we have power raised by another power, we have to multiply the powers.

= 2³⁶

Problem 9 :

Which expression is equivalent to (-4^-5)⁰ ?

a)  1       b)  (-4^-5)       c)  1/(-4^-5)     d)  1⁵/-4

Solution :

= (-4^-5)⁰

Anything to the power of 0 will be 1. Then the value of  (-4^-5)⁰ is 1.

Problem 10 :

Which expression is equivalent to (7²)⁵ / (7^-6) ?

a)  7       b)  7⁴       c)  7¹³     d)  7¹⁶

Solution :

= (7²)⁵ / (7^-6)

= 7¹⁰ / (7^-6)

Converting the negative exponent as positive exponent, we get

= 7¹⁰ (7⁶)

= 7^{10 + 6}

= 7¹⁶

Problem 11 :

Which each of the following numbers as product of whole number of 10. Then describe the relationship between the place value and exponents 

a) 3000       b)  300      c)  0.3      d)  0.003

Solution :

a)  3000

3000 = 3 x 1000

= 3 x 10³

b)  300

300 = 3 x 100

= 3 x 10²

c)  0.3

0.3 = 3 x (1/10)

= 3 x 10^-1

d)  0.003

0.003 = 3 x (1/1000)

= 3 x 10^-3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.