EXTERIOR ANGLE THEOREM WORKSHEET

Problem 1 :

Find m∠W and m∠X in the triangle given below.

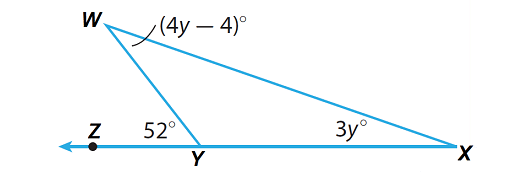
Problem 2 :

Find m∠A and m∠B in the triangle given below.

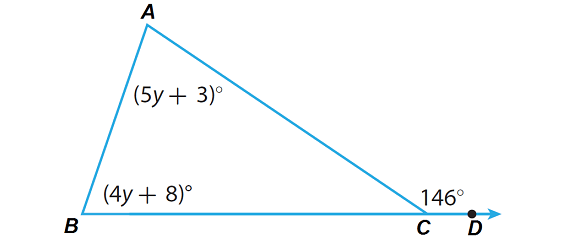
Problem 3 :

Find m∠L and m∠M in the triangle given below.

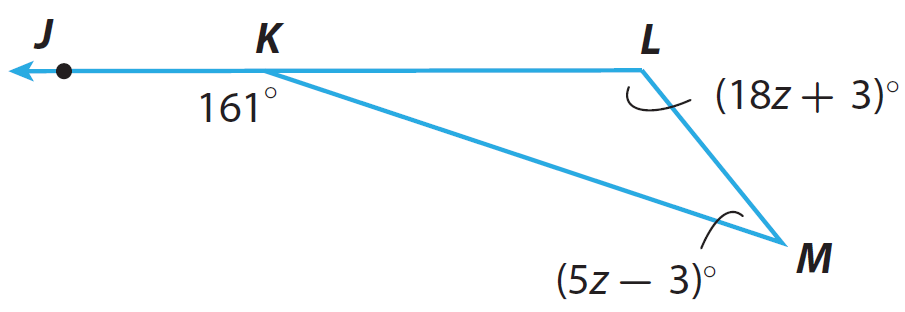
Problem 4 :

Find m∠C and m∠D in the triangle given below.

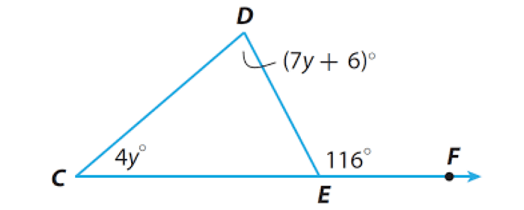
Answers

1. Answer :

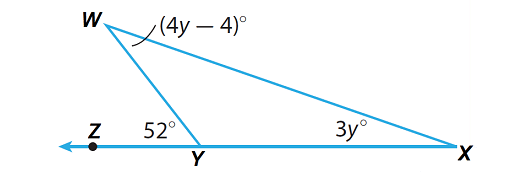
Step 1 :

Write the Exterior Angle Theorem as it applies to this triangle.

m∠W + m∠X  =  m∠WYZ

Step 2 :

Substitute the given angle measures.

(4y - 4)° + 3y°  =  52°

Step 3 :

Solve the equation for y.

(4y - 4)° + 3y°  =  52°

4y - 4 + 3y  =  52

Combine the like terms. 

7y - 4  =  52

Add 4 to both sides.

7y - 4 + 4  =  52 + 4

Simplify.

7y  =  56

Divide both sides by 7. 

7y / 7  =  56 / 7

y  =  8

Step 4 :

Use the value of y to find m∠W and m∠X.

So, m∠W  =  28° and m∠X  =  24°.

2. Answer :

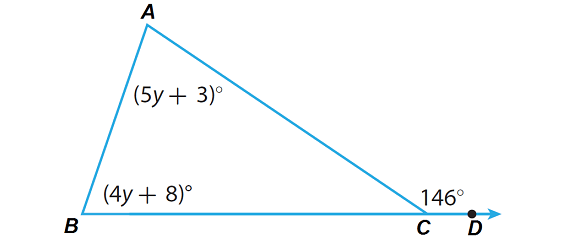
Step 1 :

Write the Exterior Angle Theorem as it applies to this triangle.

m∠A + m∠B  =  m∠C

Step 2 :

Substitute the given angle measures.

(5y + 3)° + (4y + 8)°  =  146°

Step 3 :

Solve the equation for y.

(5y + 3)° + (4y + 8)°  =  146°

5y + 3 + 4y + 8  =  146

Combine the like terms. 

9y + 11  =  146

Subtract 11 from both sides.

9y + 11 - 11  =  146 - 11

Simplify.

9y  =  135

Divide both sides by 9. 

9y / 9  =  135 / 9

y  =  15

Step 4 :

Use the value of y to find m∠A and m∠B.

So, m∠A  =  78° and m∠B  =  68°.

3. Answer :

Step 1 :

Write the Exterior Angle Theorem as it applies to this triangle.

m∠L + m∠M  =  m∠K

Step 2 :

Substitute the given angle measures.

(18z + 3)° + (5z - 3)°  =  161°

Step 3 :

Solve the equation for z.

(18z + 3)° + (5z - 3)°  =  161°

18z + 3 + 5z - 3  =  161

Combine the like terms. 

23z  =  161

Divide both sides by 23. 

23z / 23  =  161 / 23

z  =  7

Step 4 :

Use the value of z to find m∠L and m∠M.

So, m∠L  =  129° and m∠M  =  32°.

4. Answer :

Step 1 :

Write the Exterior Angle Theorem as it applies to this triangle.

m∠C + m∠D  =  m∠E

Step 2 :

Substitute the given angle measures.

4y° + (7y + 6)°  =  116°

Step 3 :

Solve the equation for y.

4y° + (7y + 6)°  =  116°

4y + 7y + 6  =  116

Combine the like terms. 

11y + 6  =  116

Subtract 6 from both sides.

11y + 6 - 6  =  116 - 6

Simplify.

11y  =  110

Divide both sides by 11. 

11y / 11  =  110 / 11

y  =  10

Step 4 :

Use the value of y to find m∠C and m∠D.

So, m∠C  =  40° and m∠D  =  76°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.