FACTORING POLYNOMIALS USING SYNTHETIC DIVISION
In this section, we use the synthetic division method that helps to factor a cubic polynomial into linear factors. If we identify one linear factor of cubic polynomial p(x) then using synthetic division we can get the quadratic factor of p(x). Further if possible one can factor the quadratic factor into linear factors.
Factor each of the following polynomials using synthetic division :
Example 1 :
x3 - 3x2 - 10x + 24
Solution :
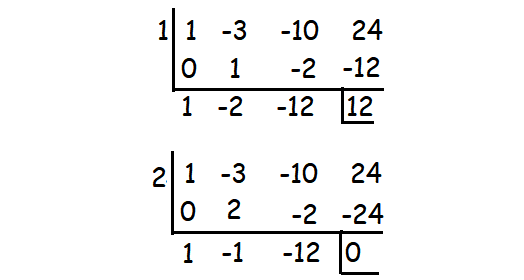
By Substituting x = 2, we get the remainder 0.
So (x - 2) is a factor.
Then,
x2 - x - 12 = x2 - 4x + 3x - 12
x2 - x - 12 = x(x - 4) + 3(x - 4)
x2 - x - 12 = (x + 3)(x - 4)
Therefore, the factors are (x - 2)(x + 3)(x- 4).
Example 2 :
2x3 - 3x2 - 3x + 2
Solution :
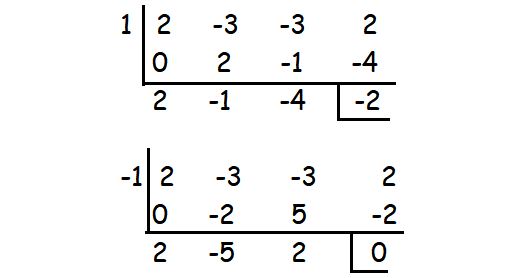
By substituting x = -1, we get the remainder 0.
So (x + 1) is a factor.
Then,
2x2 - 5x + 2 = 2x2 - 4x - x + 2
2x2 - 5x + 2 = 2x(x - 2) - 1(x - 2)
2x2 - 5x + 2 = (2x - 1)(x - 2)
Therefore, the factors are (x + 1)(2x - 1)(x - 2).
Example 3 :
-7x + 3 + 4x3
Solution :
-7x + 3 + 4x3 = 4x3 + 0x2 - 7x + 3
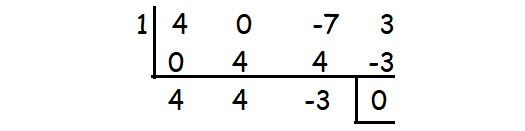
By substituting x = 1, we get the remainder 0.
So (x - 1) is a factor.
Then,
4x2 + 4x - 3 = 4x2 + 6x - 2x - 3
4x2 + 4x - 3 = 2x(2x + 3) - 1(2x + 3)
4x2 + 4x - 3 = (2x - 1)(2x + 3)
Therefore, the factors are (x - 1)(2x - 1)(2x + 3).
Example 4 :
x3 + x2 - 14x - 24
Solution :
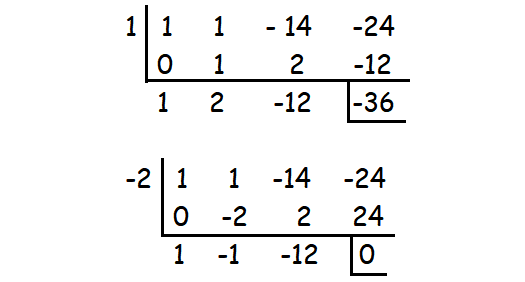
By substituting x = -2, we get the remainder 0.
So (x + 2) is a factor.
Then,
x2 - x - 12 = x2 - 4x + 3x - 12
x2 - x - 12 = x(x - 4) + 3(x - 4)
x2 - x - 12 = (x + 3)(x - 4)
Therefore, the factors are (x + 2)(x + 3)(x - 4).
Example 5 :
x3 - 7x + 6
Solution :
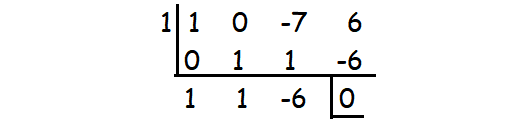
By substituting x = 1, we get the remainder 0.
So (x - 1) is a factor.
Then,
x2 + x - 6 = x2 + 3x - 2x - 6
x2 + x - 6 = x(x + 3) - 2(x + 3)
x2 + x - 6 = (x + 3)(x - 2)
Therefore, the factors are (x - 2)(x + 3)(x - 1).
Example 6 :
x3 - 10x2 - x + 10
Solution :
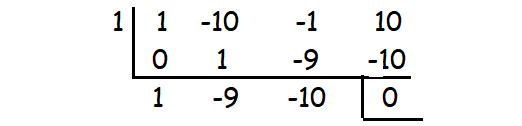
By substituting x = 1, we get the remainder 0.
So (x - 1) is a factor.
Then,
x2 - 9x - 10 = x2 - 10x + 1x - 10
x2 - 9x - 10 = x(x - 10) + 1(x - 10)
x2 - 9x - 10 = (x + 1)(x - 10)
Therefore, the factors are (x + 1)(x - 10)(x - 1).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 29)
Oct 16, 25 06:04 AM
10 Hard SAT Math Questions (Part - 29) -
10 Hard SAT Math Questions (Part - 28)
Oct 14, 25 10:57 AM
10 Hard SAT Math Questions (Part - 28) -
SAT Math Questions and Answers
Oct 13, 25 01:09 PM
SAT Math Questions and Answers