FACTORS AND MULTIPLES

Example 1 :

Find the factors of 45.

Solution :

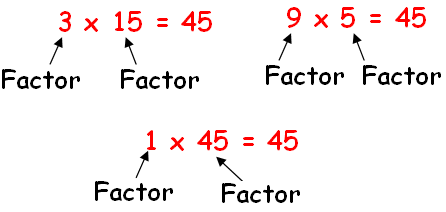
Factors of 45 are 1, 3, 5, 9, 15, 45. 

Example 2 :

18, 24 and 30 are all multiples of three.

A) True     B) False

Solution :

To check if the given numbers 18, 24 and 30 are multiples of 3 or not, we can use the divisibility rule for 3 or try to write each as product of 3.

Divisibility rule for 3 :

18 = 1 + 8 ==> 9/3 (9 is divisible by 3)

24 = 2 + 4 ==> 6/3 (6 is divisible by 3)

30 = 3 + 0 ==> 3/3 (3 is divisible by 3)

Writing it as factors of 3 :

18 = 3 x 6

24 = 3 x 8

30 = 3 x 10

So, 18, 24 and 30 are factors of 3.

Example 3 :

5 is a multiple of 20

A) True      B) False

Solution :

If we are able to write 20 as product of 5, then we decide 20 is multiple of 5.

20 = 2 x 10

20 = 4 x 5

20 is a multiple of 5.

Example 4 :

Which list is made up of multiples of 4?

A) 1, 4, 40     B) 8, 16, 36   C) 12, 22, 28    D) 4, 14, 24

Solution :

Option A :

1, 4, 40

1 is a not a multiple of 4. 4 is the first multiple of 4.

Then, let us choose option D.

Option D :

4, 14, 24

Here 4 is a multiple of 4 but 14 is not a multiple of 4. So, option D is incorrect.

Option B :

8, 16, 36

8 = 2 x 4

16 = 4 x 4

36 = 4 x 9

So, option B is correct.

Example 5 :

The multiples of 5 all end in 0 or 5.

A) True B) False

Solution :

A number which ends with 0 or 5 will be divisible by 5. Then it is true.

Example 6 :

Six has all the following factors...

A) 1, 2, 3, 6     B) 3, 6, 12, 18      C) 2, 4, 6

Solution :

Factors of 6 are,

1, 2, 3 and 6. Then option A is correct.

Example 7 :

Five has only two factors.

A) True B) False

Solution :

5 is a prime number, every prime number is divisible by 1 and itself. Then it is true.

Example 8 :

The factors of 24 include...

A) 1, 6, 9     B) 1, 8, 12    C) 1, 5, 12     D) 15, 30, 48

Solution :

Factors of 24 are,

1, 2, 3, 4, 6, 8, 12, 24

So, option B is correct.

Let us see an example to understand the above method

Example 9 :

Find the number of factors of 48

Solution :

To get the number of factors of 48, first we have to find the factors.

48  =  1 x 48

48  =  2 x 24

48  =  3 x 16

48  =  4 x 12

48  =  6 x 8

Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

Number of factors of 48 = 10

We can get the same answer in the below method too.

Step 1 :

For that, first we have to split the given number 48 as prime factors using prime factorization method.

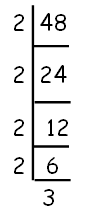
Step 2 :

48 = 2⁴ x 3¹

Take all exponents and add one to each of them. So, we get 2⁵ x 3²

Step 3 :

Multiplying the modified exponents, we get 5 x 2 = 10.

Hence, the number of factors of 48 is 10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.