FACTORS OF LINEAR EXPRESSIONS

Example 1 : 

Factor :

4x + 8

Solution : 

Find the largest common divisors for 4x and 8. 

The largest common divisor for 4x and 8 is 4. 

Divide 4x and 8 by 4

4x/4  =  x

8/4  =  2

Write the quotients x and 2 inside the parenthesis and multiply by the largest common divisor 4.

4(x + 2)

So, 

4x + 8  =  4(x + 2)

Example 2 : 

Factor :

16a + 64b - 4c

Solution : 

Find the largest common divisors for 16a, 64b and 4c. 

The largest common divisor for  16a, 64b and 4c is 4. 

Divide 16a, 64b and 4c by 4 

16a/4  =  4a, 64b / 4  =  16b and 4c / 4  =  c

Write the quotients 4a, 16b and c inside the parenthesis and multiply by the largest common divisor 4.

4(4a + 16b - c)

So,

16a + 64b - 4c  =  4(4a + 16b - c) 

Example 3 : 

Factor :

-25x + 15

Solution : 

Find the largest common divisors for 25x and 15. 

The largest common divisor for 25x and 15 is 5. 

Divide 25x and 15 by 5.

25x/5  =  5x

15/5   =  3

Write the quotients 5x and 3 inside the parenthesis and multiply by the largest common divisor 5x.

5(-5x + 3)

So,

-25x + 15  =  5(-5x + 3)

Example 4 : 

Factor :

1.5y - 9

Solution : 

Find the largest common divisors for 1.5y and  9.

The largest common divisor for 1.5y and 9. is 1.5

Divide each term by 1.5y.

1.5y/1.5  =  y 

9/1.5  =  6

Write the quotients y and 6 inside the parenthesis and multiply by the largest common divisor 1.5.

1.5(y - 6)

So, 

1.5y - 9  =  1.5(y - 6)

Example 5 : 

Factor : 

4w - 8x + 16y - 32z

Solution : 

Find the largest common divisors for 4w, 8x, 16y and 32z.

The largest common divisor 4w, 8x, 16y and 32z is 4.

Divide each term by 4.

4w/4  =  w

8x/4  =  2x

16y/4  =  4y

32z/4  =  8z

Write the quotients inside the parenthesis and multiply by the largest common divisor 4.

4(w - 2x + 4y - 8z)

So, 

4w - 8x + 16y - 32z  =  4(w - 2x + 4y - 8z)

Example 6 :

The volume of a bowling ball can be modelled by the function V(x) = 168 - 28x - 28x², where x represents the radius of the finger holes in inches. Identify the values of x for which V(x) = 0, and use the graph of factor V(x).

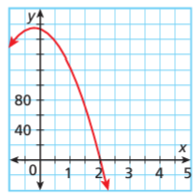
Solution : 

V(x) = 168 - 28x - 28x²

= 28(6 - x - x²)

= -28(x² - x - 6)

Factoring this quadratic polynomial, we get

-28(x² - x - 6) = 0

(x² - 3x + 2x - 6) = 0

x(x - 3) + 2(x - 3) = 0

(x + 2)(x - 3) = 0

Equating each factor to 0, we get

x + 2 = 0 and x - 3 = 0

x = -2 and x = 3

So, the required values of x are -2 and 3.

Given the volume and height, find a polynomial expression for the area of the base and dimension in terms of x for each figure.

Example 7 :

V(x) = 2x³ - 17x² + 27x + 18

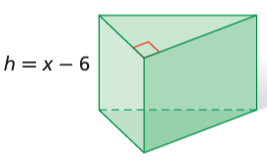
Solution :

Given that V(x) = 2x³ - 17x² + 27x + 18

Since height is given that x - 6

Dividing the cubic polynomial by linear x - 6, we get

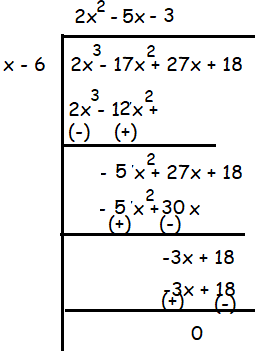
By factoring 2x² - 5x - 3

= 2x² - 6x + 1x - 3

= 2x(x - 3) + 1(x - 3)

= (2x + 1)(x - 3)

So, the dimensions are (2x + 1) (x - 3) and (x - 6).

Example 8 :

The area of the square is 4x² + 12x + 9 square units. Which expression represents the length of the side.

a)  3x + 2 units    b)  4x + 9 units

c)  2x + 3 units    d) 4x + 3 units

Solution :

4x² + 12x + 9

Factoring this polynomial,

= (2x)² + 2(2x) (3) + 3²

Looks like a² + 2ab + b² = (a + b)²

= (2x + 3)²

= (2x + 3) (2x + 3)

So, the side length of the square is 2x + 3 units.

Example 9 :

If the area of the square is (4𝑥² − 4𝑥 + 1) 𝑐𝑚², what is the measure of its side?

a.)  (−2𝑥 + 1) 𝑐𝑚      b)  (4𝑥 − 2) 𝑐𝑚 

c)   (−4𝑥 + 1) 𝑐𝑚       d) (2𝑥 − 1) cm

Solution :

Area of square = (4𝑥² − 4𝑥 + 1) 𝑐𝑚²

= (2x)² - 2(2x) (1) + 1²

= (2x - 1)²

= (2x - 1)(2x - 1)

So, the required side length of the square is 2x - 1 units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.