FIND LCM WHEN POLYNOMIALS AND GCD ARE GIVEN

Find the LCM of each pair of the following polynomials

Example 1 :

x² - 5x + 6, x² + 4 x - 12 whose GCD is (x - 2)

Solution :

LCM ⋅ GCD  =  f(x) ⋅ g(x)

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x) = x² - 5x + 6

g(x) = x² + 4x - 12

GCD  =  (x-2)

x² - 5x + 6 = (x - 2)(x - 3)

x² + 4x - 12 = (x + 6)(x - 2)

LCM  =  (x - 2)(x - 3)(x + 6)(x - 2)/(x - 2)

By canceling common factors, we get

LCM  =  (x-2) (x-3) (x+6)

So, the required LCM is (x-2) (x-3) (x+6).

Example 2 :

x⁴ + 3x³ + 6x² + 5x + 3, x⁴ + 2x² + x + 2 whose GCD is x² + x + 1

Solution :

x⁴ + 3x³ + 6x² + 5x + 3, x⁴ + 2x² + x + 2 whose GCD is x² + x + 1

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x) = x⁴ + 3x³ + 6x² + 5x + 3

g(x) = x⁴ + 2x² + x + 2

GCD = x² + x + 1

LCM  = [(x⁴ + 3x³ + 6x² + 5x + 3) (x⁴ + 2x² + x + 2) ]/(x² + x  + 1)

To simplify this, we have to use long division.

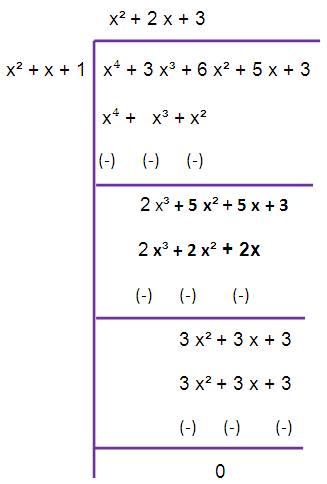
LCM  =  (x² + 2x + 3) (x⁴ + 2x² + x + 2)

So, the required LCM is (x² + 2x + 3) (x⁴ + 2x² + x + 2).

Example 3 :

2x³ + 15x² + 2x - 35, x⁴ + 8x² + 4x - 21 whose GCD is x + 7

Solution :

2x³ + 15x² + 2x - 35, x⁴ + 8x² + 4x - 21 whose GCD is x + 7

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x)  =  2x³ + 15x² + 2x - 35

g(x)  =  x⁴ + 8x² + 4x - 21

GCD  = x + 7

LCM  =  [(2x³ + 15x² + 2x - 35) (x⁴ + 8x² + 4x - 21)]/(x + 7)

To simplify this we have to use long division.

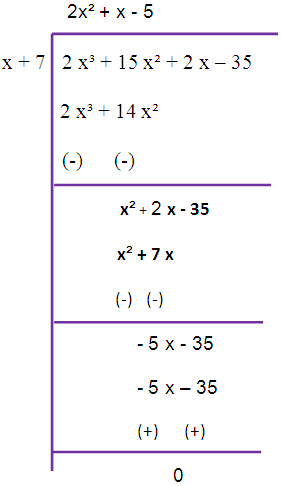
LCM  =  (2x²+x-5) (x⁴+8x²+4x-21)

So, the required LCM is  (2x²+x-5) (x⁴+8x²+4x-21).

Example 4 :

2x³ - 3x² - 9x + 5, 2x⁴ - x³ - 10x² - 11x + 8 whose GCD is 2x - 1

Solution :

2x³ - 3x² - 9x + 5, 2x⁴ - x³ - 10x² - 11x + 8 whose GCD is 2x - 1

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x)  =  2x³ - 3x² - 9x + 5

g(x)  =  2x⁴ -x³ - 10x² - 11x + 8

GCD = 2x - 1

LCM  =  [(2x³ - 3x² - 9x + 5) (2x⁴ - x³ - 10x² - 11x + 8)]/(2x - 1)

To simplify this we have to use long division.

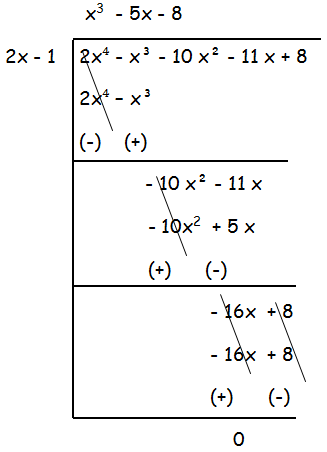
LCM  =  (x³ - 5x - 8) (2x³-3x²-9x+5)

So, the LCM is (x³ - 5x - 8) (2x³ - 3x² - 9x + 5).

Example 5 :

If (x - a) is the GCD of x² - x - 6 and x² + 3x - 18, find the value of a.

a)  3    b)  6    c)  9   d) None of these

Solution :

Since (x - a) is GCD of the given polynomials 

x² - x - 6 and x² + 3x - 18

We know that, by dividing each polynomial by x - a, we get 0 as remainder.

Let p(x) = x² - x - 6

x - a = 0

x = a

a² - a - 6 = 0

(a -3)(a + 2) = 0

a = 3 and a = -2

Accordingly the options given 3 is the value of a.

Example 6 :

Find the LCM of pair of polynomials given a² + 4a - 12, a² - 5a + 6 whose GCD is (a - 2)

Solution :

LCM ⋅ GCD  =  f(x) ⋅ g(x)

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x) = a² + 4a - 12

g(x) = a² - 5a + 6

GCD = (a - 2)

f(x) = a² + 4a - 12 = (a + 6)(a - 2)

g(x) = a² - 5a + 6 = (a - 2)(a - 3)

LCM  =  [f(x) ⋅ g(x)]/GCD

LCM  =  [ (a + 6)(a - 2) ⋅  (a - 2)(a - 3)]/ (a - 2)

By canceling common factors, we get

LCM = (a + 6) (a - 2) (a - 3)

So, the required LCM is (a + 6) (a - 2) (a - 3).

Example 7 :

Find the LCM of pair of polynomials given 

x⁴ - 27a³ x, (x - 3a)² whose GCD is (x - 3a)

Solution :

LCM ⋅ GCD  =  f(x) ⋅ g(x)

f(x) = x⁴ - 27a³ x

= x(x³ - 27a³)

= x(x³ - (3a)³)

f(x) = x(x - 3a)(x² + 3ax + 9a²)

g(x) = (x - 3a)²

GCD = (x - 3a)

LCM  =  [x(x - 3a)(x² + 3ax + 9a²) ⋅ (x - 3a)²]/(x - 3a)

=  x (x² + 3ax + 9a²) ⋅ (x - 3a)²

Example 8 :

(x -4) is the GCD of x² - x - 12 and x² - mx - 8, find the value of m

a)  4    b)  6   c)  2  d) none

Solution :

Let f(x) = x² - x - 12

g(x) = x² - mx - 8

Since x - 4 is a GCD of the given polynomials, they are divisible by this factor.

x - 4 = 0

x = 4

g(4) = 4² - m(4) - 8

0 = 16 - 4m - 8

0 = 8 - 4m

4m = 8

m = 8/4

m = 2

So, the value of m is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.