FIND MEDIAN LOWER QUARTILE UPPER QUARTILE FROM STEM AND LEAF
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :

For the data set given, find:
a) the minimum value
b) the maximum value
c) the median
d) the lower quartile
e) the upper quartile
f) the range
g) the interquartile range.
Solution :
Listing out the data from stem and leaf,
20, 21, 22, 22, 30, 30, 31, 34, 34, 35, 38, 40, 42, 43, 44, 46, 46, 49, 51, 51, 54, 55, 58
(a) Minimum value = 20
(b) Maximum value = 58
(c) Median :
Total number of data values = 23
= (23+1)/2
= 24/2
= 12th value
So, median is 40.
Since median is one of the value in the given data set, by ignoring median we can divide the given data set into two parts.
(d) Lower half :
20, 21, 22, 22, 30, 30, 31, 34, 34, 35, 38
Lower quartile (Q1) = 30
(e) Upper half :
42, 43, 44, 46, 46, 49, 51, 51, 54, 55, 58
Upper quartile (Q3) = 49
(f) Range = Large value - Small value
= 58-20
Range = 38
(g) Interquartile range :
IQR = Q3 - Q1
IQR = 49-30
IQR = 19
Example 2 :
The weight, in kilograms, of a particular brand of bags of firewood is stated to be 20 kg. However, some bags weigh more than this and some weigh less. A sample of bags is carefully weighed, and the measurements are given in the ordered stem-and-leaf plot shown.

a) Locate the median, upper and lower quartiles, and maximum and minimum weights for the sample.
b) Draw a boxplot for the data.
c) Find:
(i) the interquartile range
(ii) the range.
d) Copy and complete the following statements about the distribution of weights for the bags of firewood in this sample:
i) Half of the bags of firewood weighed at least ..... kg.
ii) .....% of the bags had a weight less than 20 kg.
iii) The weights of the middle 50% of the bags were spread over ..... kg.
iv) The lightest 25% of the bags had a weight of ..... kg or less.
e) Is the distribution of weights in this sample symmetrical, or positively or negatively skewed?
Solution :
18.8, 19.5, 19.7, 19.7, 19.8, 19.8, 19.9, 20.1, 20.1, 20.1,
20.2, 20.2, 20.5, 20.6, 20.8, 21, 21.1, 21.1, 21.2, 21.4,
21.6, 22.3
Total number of weights = 22
Median = (11th value + 12th value)/2
= (20.2+20.2)/2
= 20.2 kg
Lower half :
18.8, 19.5, 19.7, 19.7, 19.8, 19.8, 19.9, 20.1, 20.1, 20.1
Median of lower half = (19.8+19.8)/2
Lower Quartile (Q1) = 19.8 kg
Upper half :
20.5, 20.6, 20.8, 21, 21.1, 21.1, 21.2, 21.4, 21.6, 22.3
Median of upper half = (21.1+21.1)/2
Upper Quartile (Q3) = 21.1 kg
Maximum weight = 22.3 kg
Minimum weight = 18.8 kg
(b)
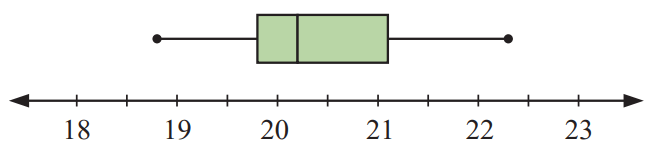
(c) Interquartile range = Q3-Q1
= 21.1 - 19.8
= 1.3
Range = Large value - small value
= 22.3 - 18.8
Range = 3.5 kg
(d)
i) Half of the bags of firewood weighed at least 20.2 kg.
ii) .....% of the bags had a weight less than 20 kg.
Number of weights less than 20 kg = 7
= (7/22) x 100%
= 31.8%
So, 31.8% of bags has weight less than 20 kg.
iii) The weights of the middle 50% of the bags were spread over 1.3 kg.
iv) The lightest 25% of the bags had a weight of 19.8 kg or less.
(e) Since the median is closer to the bottom of the box, and the whisker is shorter on the lower end of the box, so the distribution is positively skewed.
Example 3 :
For the following sample of weights (in kg) of year 10 students, find :

a) the minimum weight
b) the maximum weight
c) the number of students with a weight greater than 52 kg
d) the number of students with a weight of at least 70 kg
e) the percentage of students with a weight less than 48 kg.
Solution :
Minimum weight = 32 kg
Maximum weight = 91 kg
(c) 20 students with a weight greater than 52 kg.
(d) 5 students with a weight at least 70 kg.
(e) From the given stem and leaf, 7 data values are less than 48 kg. Total number of data values = 35
To find percentage,
= (7/35) x 100%
= 20%
So, 20% of students with the weight of 48 kg.
Example 4 :
The stem and leaf diagram shows information about the ratings of 11 footballers in a computer game
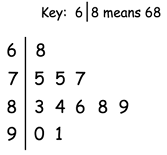
(a) How many of the footballers had a rating less than 85?
(b) Write down the mode.
(c) Work out the range of the ratings.
(d) Work out the median rating.
Solution :
(a) The data values from the stem and leaf are
68, 75, 75, 77, 83, 84, 86, 88, 89, 90, 91
Number of footballers had a rating less than 85 is 5.
b) Mode = 77
(c) Range = greater value - smaller value
= 91 - 68
= 23
(d) Median :
Total number of values = 11
Median = (11 + 1)/2th value
= 6th value
= 84 is the median.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
The 10 Hardest SAT Math Questions
Feb 04, 26 09:43 AM
The 10 Hardest SAT Math Questions -
The 10 Most Difficult SAT Math Questions
Feb 04, 26 09:14 AM
The 10 Most Difficult SAT Math Questions -
The 15 Hardest SAT Math Questions Ever
Feb 03, 26 10:47 AM
The 15 Hardest SAT Math Questions Ever


