FIND MISSING VALUE IN A QUADRATIC FUNCTION USING NATURE OF ROOTS

We can find the roots of the quadratic equation

ax² +bx +c = 0 , a ≠ 0

using the quadratic formula

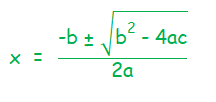
Here, b² - 4ac called as the discriminant (which is denoted by D) of the quadratic equation, decides the nature of roots as follows

Problem :

Find the value(s) of ‘k’ for which the roots of the following equations are real and equal.

(i)  (5k −6)x² + 2kx + 1 = 0

Solution :

By comparing the given quadratic equation with the general form of quadratic equation.

ax² + bx + c = 0

a = 5k-6, b = 2k  and c = 1

If the roots are real and equal, then Δ = 0

Δ = b² - 4ac

(2k)² - 4(5k-6)1  =  0

4k² - 20k + 24  =  0

k² - 5k + 6  =  0

k² - 2k - 3k + 6  =  0

k(k - 2) - 3(k - 2)  =  0

(k - 3)(k - 2)  =  0

k - 3  =  0, k - 2  =  0

k = 3, k = 2

So, the values of k are 2 or 3.

(ii)  kx² +(6k + 2)x + 16 = 0

a = k, b = 6k + 2  and c = 16

If the roots are real and equal, then Δ = 0

Δ = b² - 4ac

(6k + 2)² - 4(k)(16)  =  0

(6k)² + 2(6k)(2) + 2² - 64k  =  0

36k² + 24k + 4 - 64k  =  0

36k² - 40k  + 4  =  0

Divide by 4, we get 

9k² - 10k  + 1  =  0

9k² - 9k - k  + 1  =  0

9k(k - 1) - 1(k - 1)  =  0

(9k - 1) (k - 1)  =  0

9k - 1  =  0, k - 1  =  0

k = 1/9 or k = 1

So, the values of k are 1/9 or 1.

To know more about nature of the roots of a quadratic equation,

Please click here

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.