FIND THE AREA OF THE SHADED REGION

Find the area of shaded regions :

Example 1 :

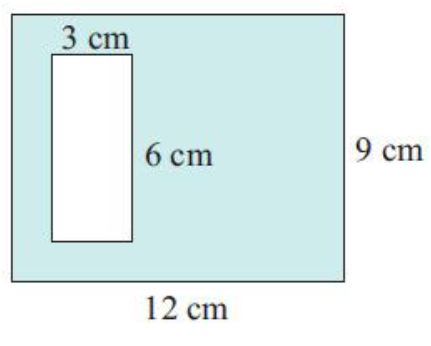
Solution :

Area of shaded region 

=  Area of large rectangle – Area of small rectangle

Area of rectangle  =  Length ⋅ width

Large rectangle :

Length  =  12 cm  

width  =  9 cm

Area of large rectangle  =  (12 ⋅ 9)

=  108 cm²------(1)

Small rectangle :

Length  =  6 cm

width  =  3 cm

Area of small rectangle  =  (6 ⋅ 3)

=  18 cm²------(2)

(1) – (2)

=  (108 – 18) cm²

=  90 cm²

So, area of shaded region is 90 cm²

Example 2 :

Solution :

Area of shaded region 

=  Area of rectangle – 2(Area of triangle)

Area of rectangle  =  length ⋅ width

Area of triangle  =  (1/2) ⋅ base ⋅ height

Area of rectangle  :

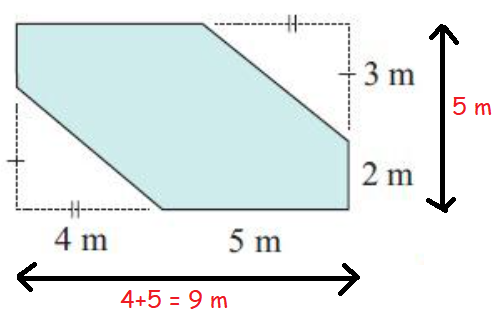
Area of rectangle  =  (9 ⋅ 5)

=  45 m²------(1)

 2(Area of triangle) :

base  =  4 m

height  =  3 m

2(Area of triangle)  =  2(1/2) ⋅ 4 ⋅ 3

=  2(6)

=  12 m²------(2)

(1) – (2)

Area of shaded region  =  (45 – 12) m²

=  33 m² 

So, area of shaded region is 33 m²

Example 3 :

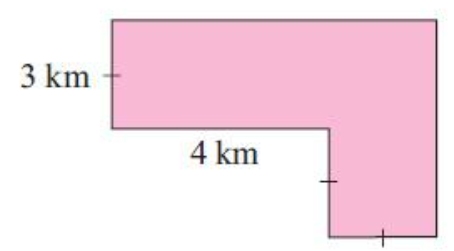
Solution :

Area of shaded region 

=  Area of rectangle + Area of square

Area of rectangle :

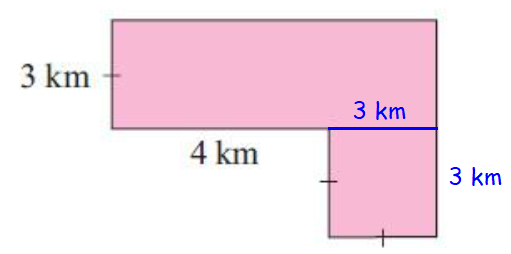
Length  =  (4 + 3) km  ==>  7 km

Width  =  3 km

Area of rectangle  =  (7 ⋅ 3)

=  21 km²-----(1)

Area of square :

side  =  3 km

Area of square  =  (side)²  =  (3)²

=  9 km²-----(2)

(1) + (2)

=  (21 + 9) km²

Area of shaded region  =  30 km²

So, area of shaded region is 30 km²

Example 4 :

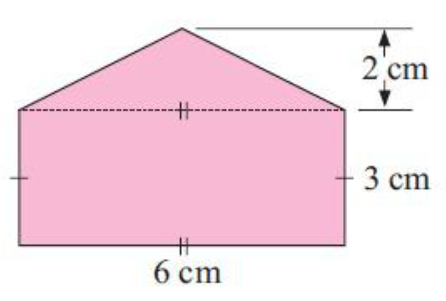
Solution :

Area of shaded region

=  Area of triangle + Area of rectangle

Area of triangle :

Area of triangle  =  (1/2) ⋅ base ⋅ height

base  =  6 cm and height  =  2 cm

Area of triangle  =  (1/2 ⋅ 6 ⋅ 2)

=  6 cm²-----(1)

Area of rectangle :

Area of rectangle  =  Length . width

Length  =  6 cm and Width  =  3 cm

Area of rectangle  =  (6 ⋅ 3)

=  18 cm²-----(2)

(1) + (2)

Area of shaded region  =  (6 + 18) cm²

=  24 cm²

So, area of shaded region is 24 cm²

Example 5 :

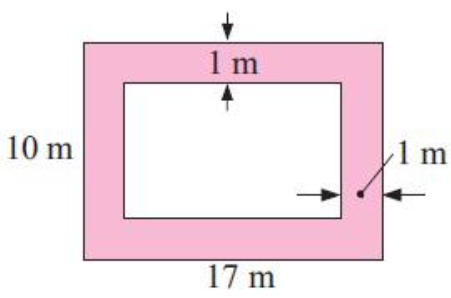
Solution :

Area of shaded region

=  Area of large rectangle – Area of small rectangle

Area of rectangle  =  Length ⋅ width

Large rectangle :

Length  =  17 m and width  =  10 m

Area of large rectangle  =  (17 ⋅ 10)

=  170 m²------(1)

Small rectangle :

Length  =  (17–2)  ==>  15 m

width  =  (10–2) ==>  8 m

Area of small rectangle  =  (15 ⋅ 8)

=  120 m²------(2)

(1) – (2)

=  (170 – 120) m²

=  50 m²

So, area of shaded region is 50 m²

Example 6 :

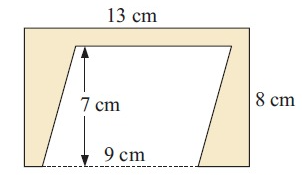
Solution :

Area of shaded region

=  Area of rectangle – Area of parallelogram

Area of parallelogram  =  base ⋅ height

Area of rectangle :

Area of rectangle  =  Length ⋅ width

Length  =  13 cm and width  =  8 cm

Area of rectangle  =  (13 ⋅ 8)

=  104 cm²-----(1)

Area of parallelogram :

base  =  9 cm and height  =  7 cm

Area of parallelogram  =  (9 ⋅ 7)

=  63 cm²------(2)

(1) – (2)

=  (104 – 63) cm²

Area of shaded region  =  41 cm²

So, area of shaded region is 41 cm²

Example 7 :

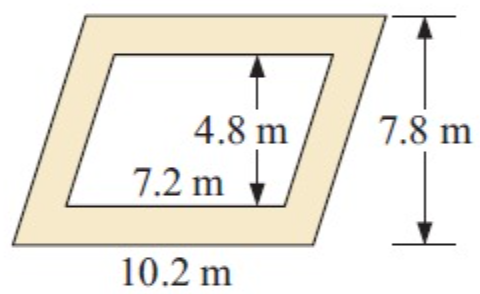
Solution :

Area of shaded region

=  Area of large parallelogram – Area of small parallelogram

Large parallelogram :

base  =  10.2 m and height  =  7.8 m

Area of large parallelogram  =  (10.2 × 7.8)

=  79.56 m²------(1)

Small parallelogram :

base  =  7.2 m and height  =  4.8 m

Area of small parallelogram  =  (7.2 × 4.8)

=  34.56 m²------(2)

(1) – (2)

=  (79.56 – 34.56) m²

=  45 m²

So, area of shaded region is 45 m²

Example 8 :

A rectangular lawn 18 m by 30 m is surrounded by a concrete path 1 m wide. Draw a diagram of the situation and find the total area of concrete.

Solution :

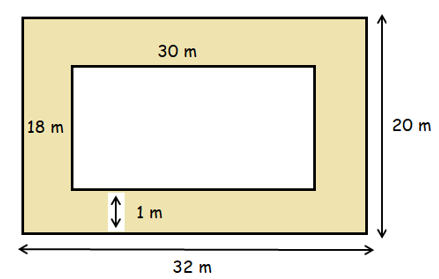
Area of shaded region

=  Area of rectangular concrete path – Area of rectangular lawn

Area of rectangle  =  Length . width

Area of rectangular concrete path :

Length  =  (30+2) m  ==>  32 m

width  =  (18+2) m  ==>  20 m

Area of rectangular concrete path  =  (32 . 20)

=  640 m²------(1)

Area of rectangular lawn :

Length  =  30 m and width  =  18 m

Area of rectangular lawn  =  (30 . 18)

=  540 m²------(2)

(1) – (2)

=  (640 – 540) m²

=  100 m²

So, total area of concrete is 100 m²

Example 9 :

The shaded square is inscribed the larger square

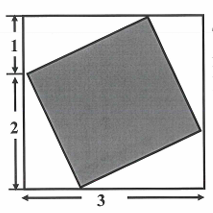
Solution :

Since the given shape is a square and at each corner we see right triangles. Each right triangle should satisfy Pythagorean theorem also,

2² + 1² = (Side length of square)²

4 + 1 = (Side length of square)²

(Side length of square)² = 5

Area of square = side length x side length

So, area of the shaded square is 5 square units.

Example 10 :

The figure consists of 2 concentric circles. If the shaded area is The shaded circle is 64 π and the smaller circle has the radius of 6 cm, what is the radius of the larger circle in inches ?

Solution :

Let R and r be the radius of larger circle and smaller circle respectively.

Area of shaded circle = Area of larger circle - area of smaller circle

= πR² - π r²

πR² - π r² = 64π

R² - r² = 64

Here r = 6

R² - 6² = 64

R² = 64 + 36

R² = 100

R = 10

So, radius of larger circle is 10 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.