FIND THE EQUATION OF THE LINE PASSING THROUGH THE POINTS

Here we are going to see how to find the equation of the line passing through the point, which is parallel or perpendicular to the given line.

Before going to see example problems, we must know the following things.

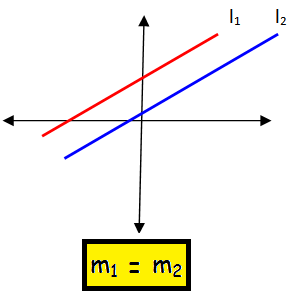
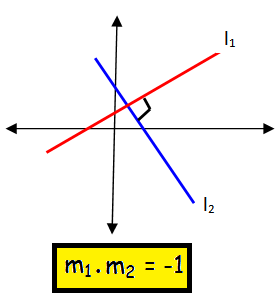
If two lines are parallel	If two lines are perpendicular

Question :

Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and (i) through the point (−1, 2) (ii) Parallel to x−y+5 = 0 (iii) Perpendicular to x − 2y+1 = 0

Answer :

4x − y + 3 = 0 -----(1) 

5x + 2y + 7 = 0-----(2) 

Multiply the first equation by 2,

8x - 2y + 6  =  0

5x + 2y + 7  =  0

------------------

13x + 13  =  0

x  =  -1

By applying x = -1 in 1st equation, we get 

4(-1) - y + 3  =  0

-4 - y + 3  =  0

-1 - y  =  0

y  =  -1

Point of intersection of given lines (-1, -1)

(i) through the point (−1, 2)

(y−y₁)/(y₂−y₁)  =  (x−x₁)/(x₂-x₁)

(y+1)/(2+1)  =  (x+1)/(-1 + 1)

(y+1)/3 = (x+1)/0

x + 1  =  0

(ii) Parallel to x−y+5 = 0

Slope of the required line  =  -1/(-1)  =  1

Passing through the point (-1, -1)

(y - y₁)  =  m (x - x₁)

(y + 1)  =  1 (x + 1)

y  =  x

x - y  = 0

(iii) Perpendicular to x − 2y + 1 = 0

m  =  -1/(-2)  =  1/2

Slope of required line  =  -2

(y + 1)  =  -2(x + 1)

y + 1 = -2x - 2

2x + y + 1 + 2  =  0

2x + y + 3  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.