FIND THE EQUATION OF THE PARABOLA WITH THE GIVEN INFORMATION

About "Find the Equation of the Parabola with the Given Information"

Find the Equation of the Parabola with the Given Information :

Here we are going to see some practice questions on find the equation of the parabola with the given information

Find the Equation of the Parabola with the Given Information - Practice questions

Question 1 :

Find the equation of the parabola in each of the cases given below:

(i) focus (4, 0) and directrix x = −4.

Solution :

From the given information, we know that the given parabola is symmetric about x-axis and it is open leftward.

Equation of the parabola with vertex (0, 0)

y²  =  4ax

Here a = 4

y²  =  4(4)x

y²  =  16x

(ii) passes through (2,-3) and symmetric about y -axis.

Solution :

Equation of the parabola which is symmetric about y-axis and open down ward

x²  =  -4ay  ----(1)

The parabola is passes through the point (2, -3)

2²  =  -4a(-3)

4  =  12a

a  =  4/12

a  =  1/3

By applying the value of a in (1), we get

 x²  =  -4(1/3)y

 3x²  =  -4y

(iii) vertex (1,-2) and focus (4,-2).

Solution :

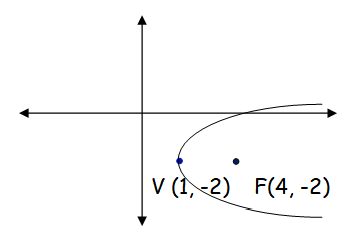
The parabola is symmetric about x axis and open right ward.

(y - k)²  =  4a(x   - h)

Here (h, k) ==>  (1, -2) and F (4, -2)

Distance between vertex and focus  =  a

a  =  √(1 - 4)² + (-2 + 2)²

a  =  3

(y + 2)²  =  4(3)(x   - 1)

(y + 2)²  =  12(x   - 1)

(iv) end points of latus rectum(4,-8) and (4,8) .

Solution :

Latus rectum must be perpendicular to the axis of parabola.

Distance between endpoints of latus rectum.

a  =  √(4 - 4)² + (-8 - 8)²

a  =  √16

a  =  4

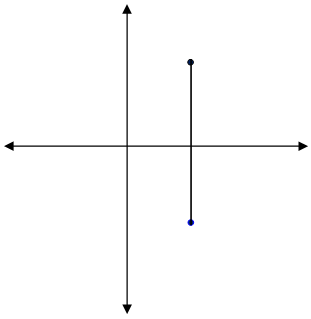
The parabola is symmetric about x-axis.

The parabola is passing through the points (4, -8) and (4, 8) 

(-8 - k)²  =  4(4)(4   - h)

(-8 - k)²  =  16(4 - h)  ----(1)

(8 - k)²  =  4(4)(4 - h)

(8 - k)²  =  16(4 - h) ----(2)

(1)  =  (2)

(8 + k)²  =  (8 - k)²

64 + 16k + k²  =  64 + k² - 16k

-32k  =  0

 k  =  0

By applying k = 0 in (1), we get 

(-8)²  =  16(4 - h)

64/16   =  4 - h

4 - h  =  4

-h  =  4 - 4

h  =  0

(y - 0)²  =  4(4)(x - 0)

y²  =  16x

After having gone through the stuff given above, we hope that the students would have understood, "Find the Equation of the Parabola with the Given Information".

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.