FIND THE OTHER ROOTS OF THE POLYNOMIAL EQUATION OF DEGREE 6

About "Find the Other Roots of the Polynomial Equation of Degree 6"

Find the Other Roots of the Polynomial Equation of Degree 6 :

Here we are going to see some example problems of solving polynomial of degree 6.

Find the Other Roots of the Polynomial Equation of Degree 6 - Practice questions

Question 1 :

Find all zeros of the polynomial x⁶ − 3x⁵ − 5x⁴ + 22x³ − 39x² − 39x + 135, if it is known that 1 + 2i and √3 are two of its zeros.

Solution :

The four roots are 1 + 2i, 1 - 2i, √3 and -√3.

Quadratic equation whose roots are 1 + 2i and 1 - 2i.

Sum of roots  =  2

Product of roots  =  1 + 4  =  5

x² - 2x + 5

Sum of roots   =  0

Product of roots  =  -3

(x² - 3) is a factor.

(x² - 2x + 5) (x² - 3)  =  x⁴ - 3x² - 2x³ + 6x + 5x² - 15

  =  x⁴ - 2x³ + 2x² + 6x - 15

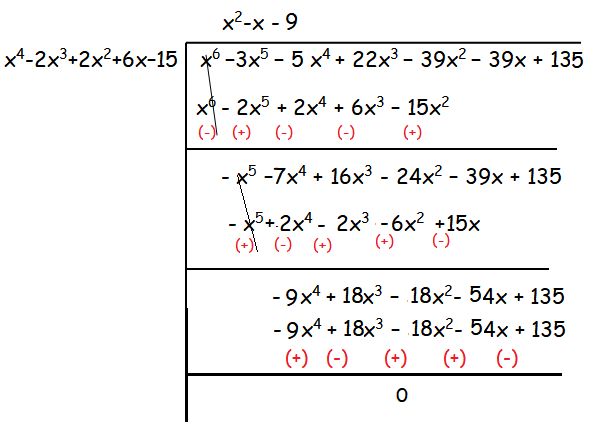
x² - x - 9  =  0

x = (-b ± √b² - 4ac)/2a

x = (1 ± √1 + 36)/2

x = (1 ± √37)/2

Hence the zeroes are 1 + 2i, 1 - 2i, √3, -√3, (1 ± √37)/2.

Question 2 :

Solve the cubic equation

(i) 2x³ − 9x² +10x = 3

Solution :

2x³ − 9x² +10x - 3  =  0

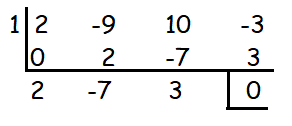
(x -1) is a factor

  =  2x² - 7x + 3  

  =  2x² - 1x - 6x + 3  

  =  x(2x - 1) - 3(2x - 1)

  =  (x - 3) (2x - 1)

(x - 1) (x - 3) (2x - 1)  =  0

x - 1  =  0, x - 3  =  0,  2x - 1  =  0

x  =  1, x  =  3, x  =  1/2

Hence the solutions are 1, 3 and 1/2.

(ii)  8x³ − 2x² − 7x + 3 = 0.

Solution :

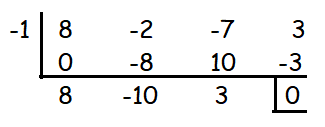
(x + 1) is a factor.

The other factors are 8x² - 10x + 3

  =  8x² - 12x + 2x + 3

  =  4x(2x - 3) -1(2x - 3)

  =  (4x - 1) (2x - 3)

By equating them to zero, we get 

x + 1  =  0, 4x - 1  =  0,  2x - 3  =  0

x  =  -1, x  =  1/4,  x  =  3/2

Hence the solutions are -1, 1/4 and 3/2.

Question 3 :

Solve the equation x⁴ −14x² + 45 = 0

Solution :

Let x²  =  t

t² − 14t + 45 = 0

t² − 9t - 5t + 45 = 0

t(t - 9) - 5(t - 9)  =  0

(t - 5) (t - 9)  =  0

t  =  5 and t  =  9

x²  =  5, x²  =  9

x  =  ±√5, x = ±3

Hence the solutions are √5, -√5, 3 and -3.

After having gone through the stuff given above, we hope that the students would have understood, "Find the Other Roots of the Polynomial Equation of Degree 6".

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.