FIND THE QUOTIENT OF RATIONAL EXPRESSIONS

How to divide the rational expressions ?

If A/B and C/D are rational expressions and B, C and D are non-zero then,

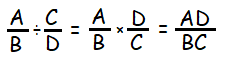
Step 1 :

If the given two rational expressions are in division, the first expression will be multiplied by the reciprocal of the second expression.

Step 2 :

Simplify the numerators and denominators in step 1.

Step 3 :

The result will be the lowest form if possible.

Note :

Sometimes it may be necessary to use factorization and algebraic identities.

Problem 1 :

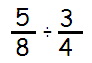
Solution :

Keep the first fraction as it is, next change the division sign as multiplication and write the reciprocal of the second fraction.

= (5/8) x (4/3)

Simplifying 4 and 8 using 4 times table, we get

= (5/2) x (1/3)

= 5/6

After we did the possible simplification, the answer is 5/6.

Problem 2 :

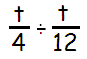
Solution :

Keep the first fraction as it is, next change the division sign as multiplication and write the reciprocal of the second fraction.

= (t/4) x (12/t)

= 12/4

Simplifying using 4 times table, we get

= 3/1

= 3

After we did the possible simplification, the answer is 3.

Problem 3 :

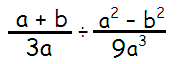
Solution :

a² - b² = (a + b)(a - b)

= [(a + b) / 3a] x [9a³ / (a + b)(a - b)]

= 3a² / (a - b)

Problem 4 :

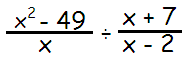
Solution :

a² - b² = (a + b)(a - b)

x² - 7² = (x + 7)(x - 7)

= [(x + 7)(x - 7) / x] ÷ [(x + 7) / (x - 2)]

Changing the division as multiplication and writing the second fraction as its reciprocal.

= [(x + 7)(x - 7) / x] ⋅ [(x - 2) / (x + 7)]

= (x - 7)(x - 2)/x

Problem 5 :

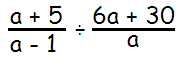
Solution :

Factoring 6 from, we get

6 a + 30 = 6(a + 5)

= [(a + 5) / (a - 1)] ÷ [6(a + 5) / a] 

= [(a + 5) / (a - 1)] x [a / 6(a + 5)] 

Cancelling (a + 5), we get

= a / 6(a - 1)

Problem 6 :

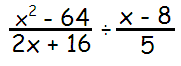
Solution :

a² - b² = (a + b)(a - b)

x² - 64 = x² - 8² = (x + 8)(x - 8)

2x + 16 = 2(x + 8)

= [(x + 8)(x - 8)/2(x + 8)] ÷ [(x - 8) / 5]

= [(x + 8)(x - 8)/2(x + 8)] ⋅ [5 / (x - 8)]

After cancelling common factors, we get

= 5/2

Problem 7 :

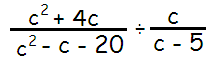
Solution :

Factoring 4, from c² + 4c, we get

c² + 4c = c(c + 4)

c² - c - 20 = (c - 5)(c + 4)

= c(c + 4) / (c - 5)(c + 4) ÷ [c/(c - 5)]

= c(c + 4) / (c - 5)(c + 4) ⋅ (c - 5)/c

After cancelling the common factors, we get

= 1

Problem 8 :

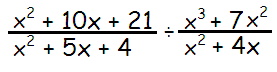
Solution :

x² + 10x + 21 = (x + 3)(x + 7)

x² + 5x + 4 = (x + 1)(x + 4)

x² + 4x = x(x + 4)

x³ + 7x² = x²(x + 7)

= [(x + 3)(x + 7)/(x + 1)(x + 4)] ÷ [ x²(x + 7) / x(x + 4)]

= [(x + 3)(x + 7)/(x + 1)(x + 4)] ⋅ [ x(x + 4) / x²(x + 7)]

= (x + 3)/x(x + 1)

Problem 9 :

Simplify the complex fraction.

[(x + 3)² / (x² - 16)] ÷ [(x + 3)/(x + 4)]

Solution :

= [(x + 3)² / (x² - 16)] ÷ [(x + 3)/(x + 4)]

= [(x + 3)(x + 3) / (x² - 4²)] ⋅ [(x + 4) / (x + 3)]

= [(x + 3)(x + 3) / (x + 4)(x - 4)] ⋅ [(x + 4) / (x + 3)]

= (x + 3) / (x - 4)

Problem 10 :

What is the volume of the rectangular prism :

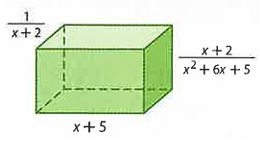
Solution :

Length of the rectangular prism = (x + 2)/(x² + 6x + 5)

Width = x + 5

Height = 1/(x + 2)

Volume of the rectangular prism = length x width x height

= (x + 2)/(x² + 6x + 5) ⋅ (x + 5) ⋅ 1/(x + 2)

= [(x + 2)/(x + 1)(x + 5)] ⋅ [(x + 5)/1] ⋅ [1/(x + 2)]

= 1/(x + 1)

So, the required volume of the rectangular prism is 1/(x + 1).

Problem 11 :

[(x - 5) / x]  ⋅  [x² / (x² - 2x - 15)]

Solution :

= [(x - 5) / x]  ⋅  [x² / (x² - 2x - 15)]

x² - 2x - 15 = (x - 5)(x + 3)

= [(x - 5) / x]  ⋅  [x² / (x - 5)(x + 3)]

= x / (x + 3)

Problem 12 :

(a² + 7a + 10) / (a + 1) ⋅ (3a + 3)/(a + 2)

Solution :

= (a² + 7a + 10) / (a + 1) ⋅ (3a + 3)/(a + 2)

a² + 7a + 10 = (a + 3)(a + 7)

3a + 3 = 3(a + 1)

= [(a + 3)(a + 7) / (a + 1)] ⋅ [3(a + 1) / (a + 2)]

= 3 (a + 3)(a + 7) / (a + 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.