FIND THE VERTEX OF ABSOLUTE VALUE EQUATIONS

In general, the graph of the absolute value function

f (x) = a| x - h| + k

is a shape "V" with vertex (h, k).

To graph the absolute value function, we should be aware of the following terms.

Horizontal Shift :

Let us consider two different functions,

y = |x| and y = |x-1|

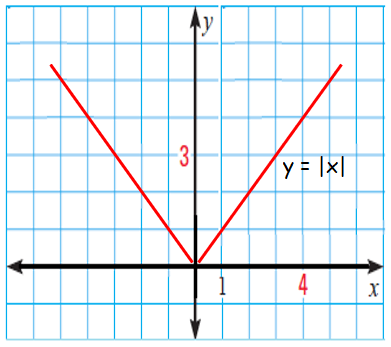
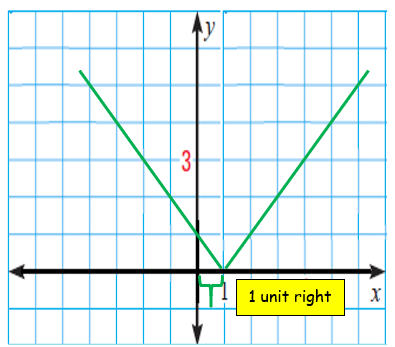
Vertex of the absolute value function y = |x| is (0, 0).

Vertex of the absolute value function y = |x-1| is (1, 0).

By comparing the above two graphs, the second graph is shifted 1 unit to the right. Since the value h is > 0, we have to move the graph h units to the right side.

Conclusion :

If h > 0, move the graph h units to the right.

If h < 0, move the graph h units to the left.

Vertical Shift :

Let us consider two different functions,

y = |x| and y = |x| + 1

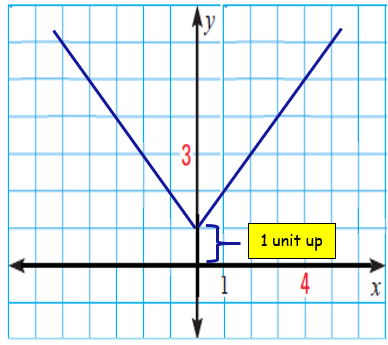
Vertex of the absolute value function y = |x| is (0, 0).

Vertex of the absolute value function y = |x|+1 is (0, 1).

Instead of k, we have +1. So, we have to move the graph 1 unit up.

If the value of k is -1. We have to move the graph 1 unit down.

Conclusion :

If k > 0, move the graph k units up.

If k < 0, move the graph k units down.

Stretch and Compression :

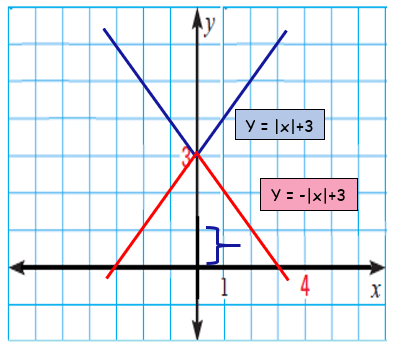
Let us consider two different functions,

y = |x| + 3 and y = -|x|+3

Graph the following absolute value function.

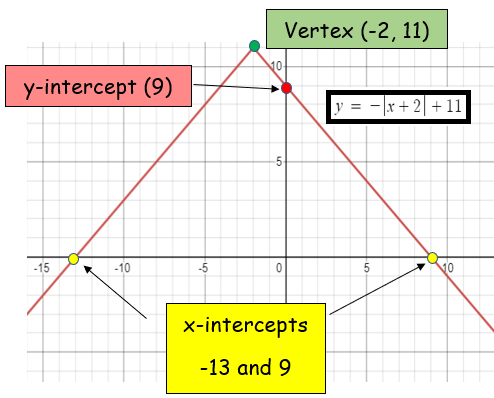
Example 1 :

y = -|x + 2| + 11

Solution :

To graph, let us find the following.

By comparing the given absolute value function with

y = |x - h| + k

Vertex (h, k) :

(-2, 11)

Horizontal Translation :

h = -2

Move the graph two units to the left.

Vertical Translation :

k = 11

Move the graph 11 units up.

Stretches and Compressions :

a = -1

x-intercept :

Put y = 0.

0 = -|x + 2| + 11

-11 = -|x + 2|

|x + 2| = 11

(x + 2) = 11 and (x + 2) = -11

x = 9 and x = -13

y-intercept :

Put x = 0.

y = -|0 + 2| + 11

y = -2 + 11

y = 9

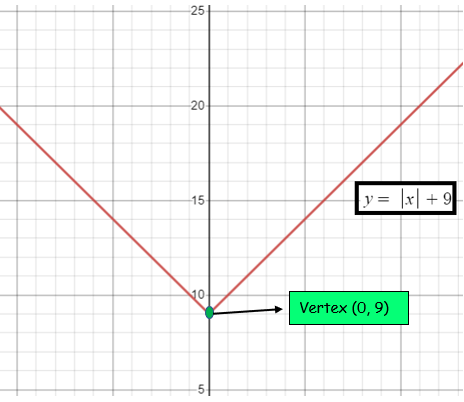
Example 2 :

y = |x| + 9

Solution :

To graph, let us find the following.

By comparing the given absolute value function with

y = |x - h| + k

Vertex (h, k) :

(0, 9)

Horizontal Translation :

h = 0

So, no horizontal shift.

Vertical Translation :

k = 9

Move the graph 9 units up.

Stretches and Compressions :

a = 1

x-intercept :

Put y = 0.

0 = |x| + 9

-9 = |x|

This will not happen, for any value of x we will not get the answer -9. So, it has no x-intercepts.

y-intercept :

Put x = 0.

y = |0| + 9

y = 9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

FIND THE VERTEX OF ABSOLUTE VALUE EQUATIONS

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Digital SAT Math Problems and Solutions (Part - 90)

Digital SAT Math Problems and Solutions (Part - 89)