FINDING ANGLES IN OTHER QUADRANTS USING REFERENCE ANGLES

The reference angle is the acute angle formed between the terminal arm and the x-axis. The reference angle is always positive and measures between 0° and 90°.

To determine the other angles in other quadrants using reference angles and the following table.

The reference angle always be lesser than 90 degree.

Question 1 :

Copy and complete the table. Determine the measure of each angle in standard position given its reference angle and the quadrant in which the terminal arm lies.

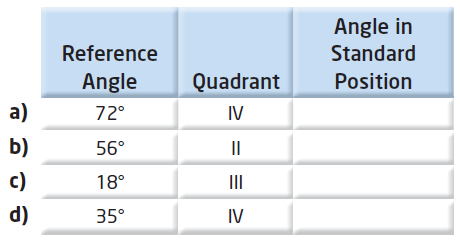
Solution :

(a)  72

Let θ be given angle.

Required angle in 4^th quadrant  =  360 - θ 

  =  360 - 72  =  288

Hence the required angle is 288.

(b)  56

Let θ be given angle.

Required angle in 2^nd quadrant  =  180 - θ 

  =  180 - 56  =  124

Hence the required angle is 124.

(c)  18

Let θ be given angle.

Required angle in 3^rd quadrant  =  180 + θ 

  =  180 + 18  =  198

Hence the required angle is 198.

(d)  35

Let θ be given angle.

Required angle in 4^th quadrant = 360 - θ 

  =  360 - 35

= 325

Hence the required angle is 325.

Question 2 :

Use the reference angle to find the EXACT VALUE of each trigonometric function.

a)  sin 225° 

Solution :

sin 225°

Here the given angle lies in third quadrant, so the reference angle will be 

= given angle - 180°

= 225° - 180°

= 45°

Using ASTC, for the trigonometry ratios tan θ and its reciprocal cot θ will be positive, the other trigonometric ratios will be negative.

sin 225° = -sin 45°

= -√2/2

b) cos 300°

Here the given angle lies in fourth quadrant, so the reference angle will be 

= 360 - given angle

= 360° - 300°

= 60°

Using ASTC, for the trigonometry ratios cos θ and its reciprocal sec θ will be positive, the other trigonometric ratios will be negative.

cos 300° = cos 60°

= 1/2

c) tan 405°

405 = 360 + 45

So, the angle lies in first quadrant.

tan 405 = tan 45

= 1

d) sec 150°

Here the given angle lies in second quadrant. So, the reference angle will be 

= 180 - given angle

= 180 - 150

= 30

Using ASTC, the value for the trigonometry ratios sin θ and its reciprocal cosec θ, we have positive. 

sec 150 = -sec 30

= -1/cos 30

= -1/√3/2

= -2/√3

e) cosec 240°

Here the given angle lies in third quadrant. So, the reference angle will be 

= given angle - 180

= 240 - 180

= 60

Using ASTC, the value for the trigonometry ratios tan θ and its reciprocal cot θ, we have positive. 

cosec 240° = -cosec 60°

= -1/sin 60

= -1/(√3/2)

= -2/√3

f) cot 210°

Here the given angle lies in third quadrant. So, the reference angle will be 

= given angle - 180

= 210 - 180

= 30

Using ASTC, the value for the trigonometry ratios tan θ and its reciprocal cot θ, we have positive. 

cot 210° = cot 30°

= 1/tan 30

= 1/(1/√3)

= √3

= -2/√3

g)  sin 240°

Here the given angle lies in third quadrant. So, the reference angle will be 

= given angle - 180

= 240 - 180

= 60

Using ASTC, the value for the trigonometry ratios tan θ and its reciprocal cot θ, we have positive. 

sin 240° = -sin 60°

= -√3/2

h)  tan 225°

Here the given angle lies in third quadrant. So, the reference angle will be 

= given angle - 180

= 225 - 180

= 45

Using ASTC, the value for the trigonometry ratios tan θ and its reciprocal cot θ, we have positive. 

tan 225° = tan 45°

= 1

Question 3 :

Prove that tan 225 cot 405 + tan 765 cot 675 = 0

Solution :

tan 225 cot 405 + tan 765 cot 675

225 lies in third quadrant, 

tan 225 = tan (225 - 180)

= tan 45

= 1

405 lies in 360 + 45 first quadrant.

cot 405 = cot 45

= 1

765 lies in 360 + 45 first quadrant.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.