FINDING AREA OF UNSHADED REGION

Find the areas of the unshaded regions:

Problem 1 :

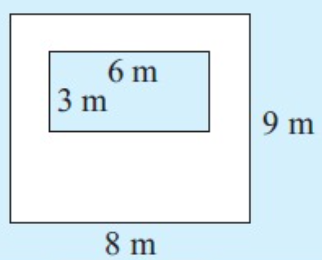
Solution :

In the picture given above, we have two rectangles. To find area of unshaded region,

=  Area of large rectangle - Area of smaller rectangle

=  9 x 8  -  6 x 3

=  72 - 18

=  54 m²

Problem 2 :

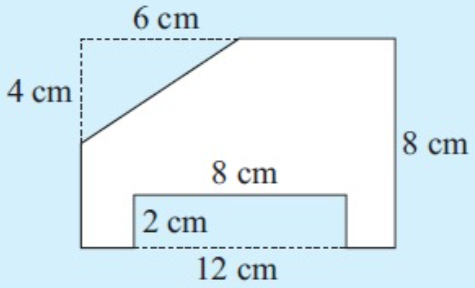
area of unshaded region  =  Area of large rectangle – area of triangle – area of small rectangle

=  l w – (1/2) b h – l w

=  12 x 8  – (1/2) x 6 x 4 – 2 x 8

=  96 – 12 - 16

=  68 cm²

So, area of unshaded region is 68 cm²_.

Problem 3 :

Chelsea measures the windows in her flat so she can calculate the length of curtain track that she needs to buy. Her measurements are 1.2 m , 1.2 m , 1.8 m , 90 cm and 45 cm. how many meter of track does Chelsea need ?

Solution :

Given Measurements are, 1.2 m , 1.2 m , 1.8 m , 90 cm and 45 cm

Converting cm to meters.

So , 90 cm  =  0. 9 m and 45 cm  =  0. 45

Perimeters  =  sum of the length of its all sides

=  1. 2 + 1. 2 + 1. 8 + 0. 9 + 0. 45

=  5. 55 m

So, Chelsa needs 5.55 m of track.

Problem 4 :

A rug measuring 2.5 m by 3.5 m was places in a room 6.4 m long and 8.2 m wide . what area of floor is not covered by the rug ?

Solution :

Area  =  l x w

Here , l  =  2.5 m and w  =  3.5 m

Area of rug  =  2.5 x 3.5

A  =  8.75 m²

l  =  6.4 m and w =  8.2 m

Area of floor  =  6.4 x 8.2

A  =  52.48 m²  

Area of floor is greater than the area of rug. So, rug cannot cover the floor.

To find the area not covered by the rug

=  52.48 - 8.75

=  43.73 m²

Problem 5 :

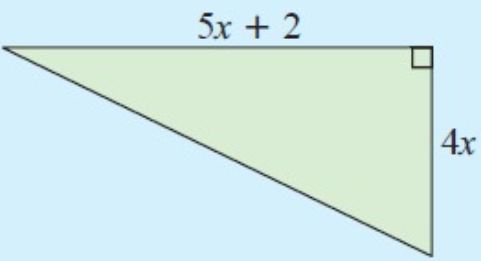
Solution :

Base of the triangle  =  5x+2

Height  =  4x

Area of green shaded region  =  Area of triangle 

=  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ (5x+2) ⋅ 4x

=  2x(5x+2)

=  10x² + 4x

Area of shaded region is (10x² + 4x) m.

Problem 6 :

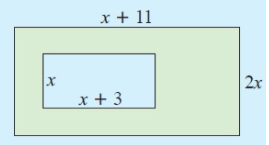
Solution :

Area of green shaded region  =  Area of large rectangle - Area of small rectangle

=  (x+11) ⋅ 2x - (x+3) ⋅ x

=  2x²+22x-3x²-3x

=  -x²+19x

Problem 7 :

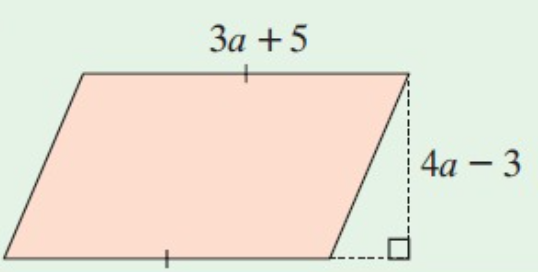
Solution :

Area of parallelogram  =  Base x Height

Base  =  3a+5 and height  =  4a-3

=  (3a+5)(4a-3)

=  12a²-9a+20a-15

=  12a²+20a-15

Problem 8 :

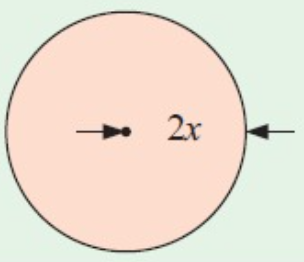
Solution :

Area of circle  =  πr²

=  π(2x)²

=  4πx²

Area of circle is 4πx².

Problem 9 :

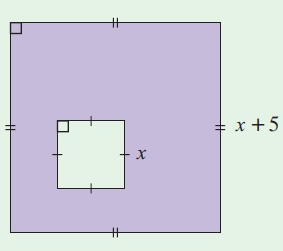
Solution :

Area of shaded region  =  Area of large square - Area of small square

A  =  l w – s²

=  (x + 5) · (x + 5) – x²

=  x² + 5x + 5x + 25 – x²

A  =  10x + 25

Area of shaded region in purple colour is (10x+25) m.

Problem 10 :

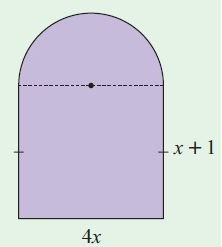
Solution :

Area A =  area of rectangle + area of semicircle

A  =  l w + πr²/2

A  =  4x · (x+1) + πr²/2

=  4x² + 4x + π (2x)²/2

=  4x² + 4x + 4πx² /2

=  4x² + 4x + 2πx²

Problem 11 :

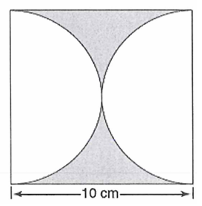
Solution :

Area of the shaded region = Area of square - 2(area of semicircles)

= a² - 2(πr²/2)

Side length of square = 10 cm

Diameter of circle = 10 cm

radius = 5 cm

= 10² - π(5)²

= 100 - 3.14(25)

= 100 - 78.5

= 21.5 cm²

Problem 12 :

A figure consists of 2 concentric circles. If the shaded is 64π square inches the smaller circle has the radius of 6 inches, what is the radius in inches of the larger circle ?

Solution :

Area of shaded region = Area of larger circle - area of smaller circle

= πR² - πr²

= π(R² - r²)

64π = π(R² - r²)

R² - r² = 64

Radius of smaller circle (r) = 6 cm

R² - 6² = 64

R² - 36 = 64

R² = 64 + 36

R² = 100

R = 10 cm

So, radius of larger circle is 10 cm.

Problem 13 :

The shaded square is inscribed in the larger circle.

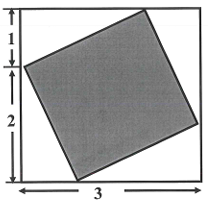
Solution :

Area of inscribed square = Area of large square - 4 (area of right triangles)

Height of the triangle = 2 cm 

base of the triangle = 1 cm

= (1/2) x base x height

= (1/2) x 2 x 1

= 1 square cm

= 3² - 4(1)

= 9 - 4

= 5 square cm.

Problem 14 :

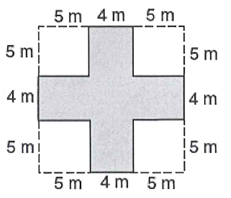
Solution :

Area of shaded region = area of large square - 4(area of squares in 4 corners)

Side length of square = 5 + 4 + 5

= 14 m

side length of small squares in 4 corners = 5 m

Required area = 14² - 5²

= 196 - 25

= 171 square meter.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.