FINDING INVERSE OF 3X3 MATRIX EXAMPLES

Let A be a square matrix of order n. If there exists a square matrix B of order n such that

AB  =   BA  =  I_n

then the matrix B is called an inverse of A.

Note :

Let A be square matrix of order n. Then, A⁻¹ exists if and only if A is non-singular.

Formula to find inverse of a matrix

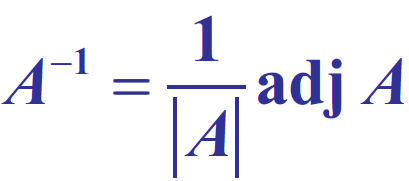
Finding Inverse of 2 x 2 Matrix

Example 1 :

Find the inverse (if it exists) of the following:

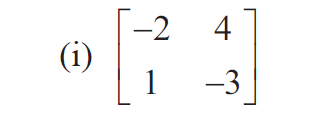
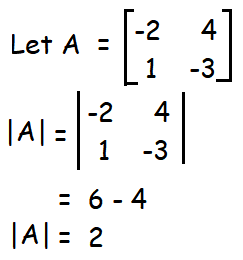
Since |A|  =  2 ≠ 0, it is non singular matrix. A^-1 exists.

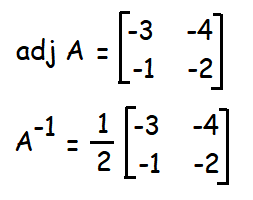
Finding the Inverse of a 3x3 Matrix Examples

Example 2 :

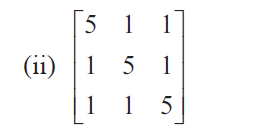
Solution :

In order to find inverse of a matrix, first we have to find |A|.

|A|  =  5(25 - 1) - 1(5 - 1) + 1(1 - 5)

  =  5(24 ) - 1(4) + 1(-4)

  =  120 - 4 - 4

  =  112

Since |A|  =  112 ≠ 0, it is non singular matrix. A^-1 exists.

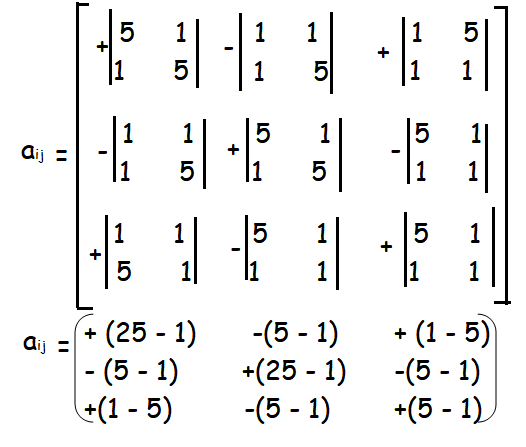
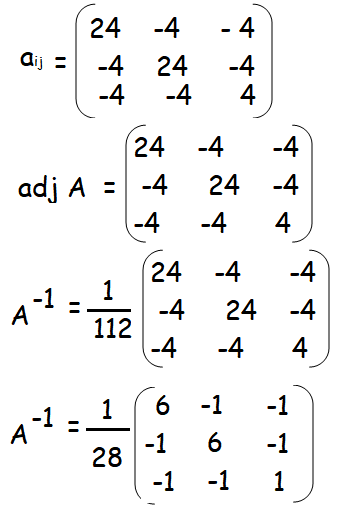
Example 3 :

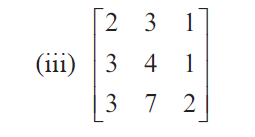
Solution :

In order to find inverse of a matrix, first we have to find |A|.

|A|  =  2(8 - 7) - 3(6 - 3) + 1(21 - 12)

  =  2(1) - 3(3) + 1(9)

  =  2 - 9 + 9

  =  2

Since |A|  =  2 ≠ 0, it is non singular matrix. A^-1 exists.

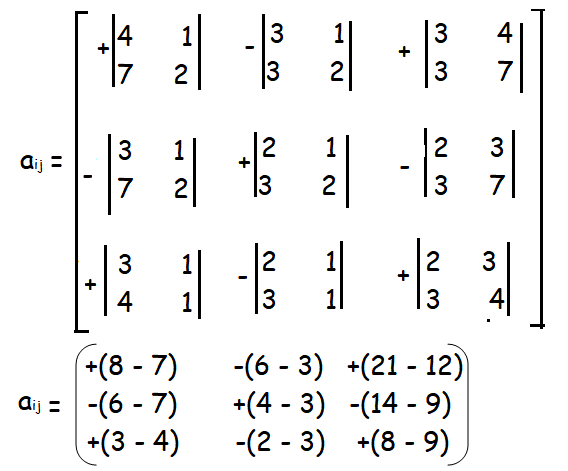
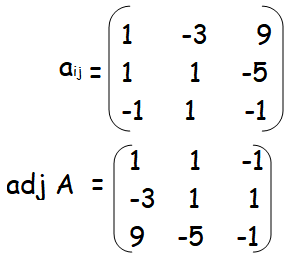
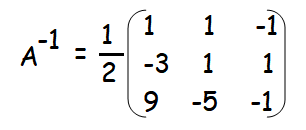
Example 4 :

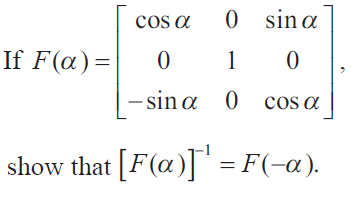
Solution :

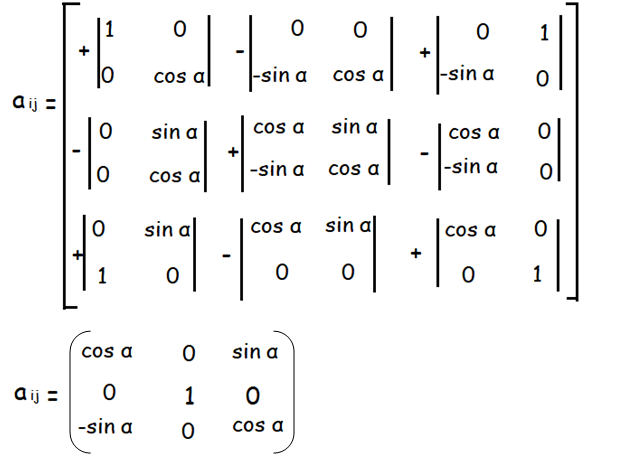
Let A  =  F(α)

A^-1 =  (1/|A|) adj A

|A|  =  cos α [cos α - 0] - 0[0 - 0] + sin α[0 + sin α]

  =  cos²α + sin²α

|A|  =  1

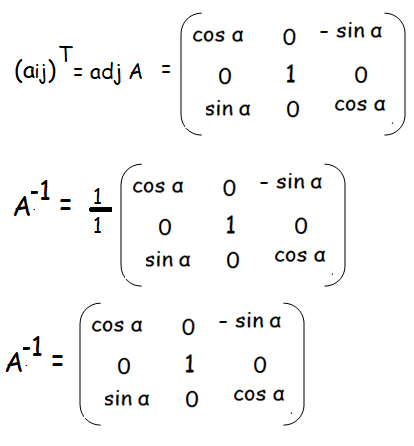
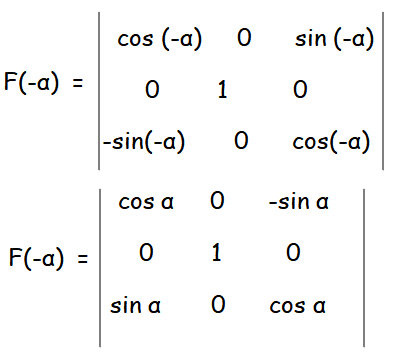
Hence proved.

Example 5 :

Solution :

  =  A² - 3A - 7I₂

Finding the value of A² :

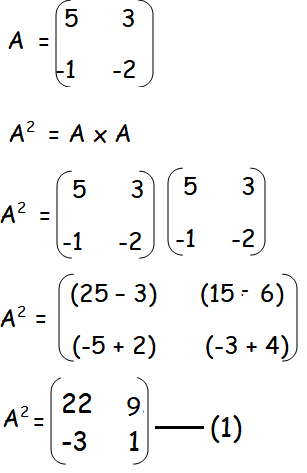
Finding the value of 3A :

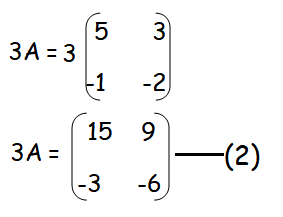
Finding the value of 7I₂ :

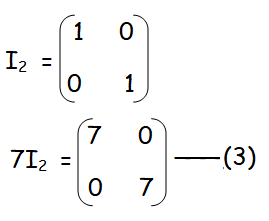
A² - 3A - 7I₂ 

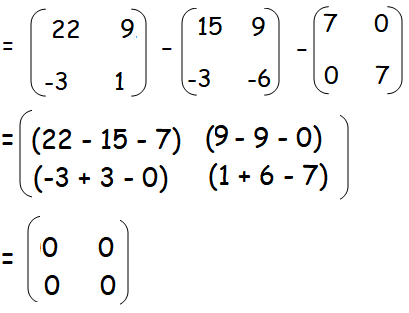
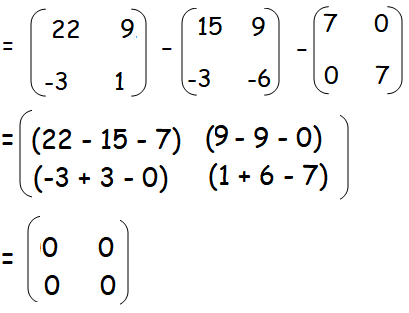
Hence proved.

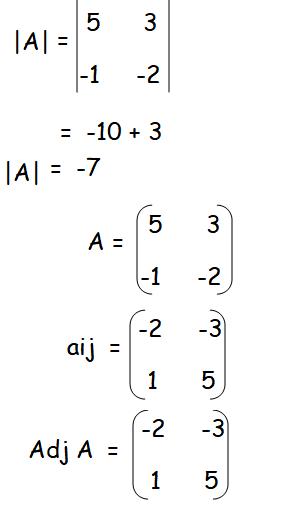
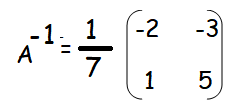
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.