FINDING LCM AND HCF OF POLYNOMIALS

Question 1 :

Find the least common multiple of xy(k² +1)+k(x² + y²) and xy(k² −1)+k(x² −y²)

Solution :

Let p(x) = xy(k² +1) + k(x² + y²) and

q(x)  =  xy(k² −1) + k(x² −y²)

L.C.M  =  (ky + x)((kx)² - y²)

L.C.M  =  (ky + x) (k²x² - y²)

Question 2 :

Find the GCD of the following by division algorithm

2x⁴ +13x³ +27x² + 23x + 7 , x³ + 3x² + 3x + 1 , x² + 2x + 1

Solution :

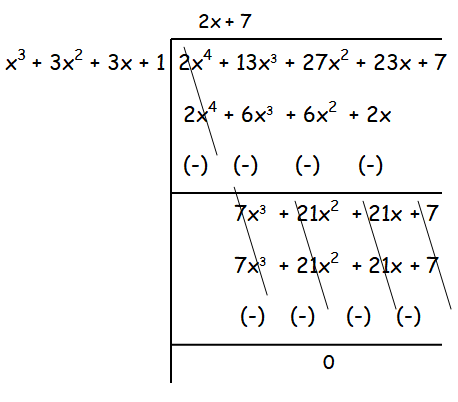
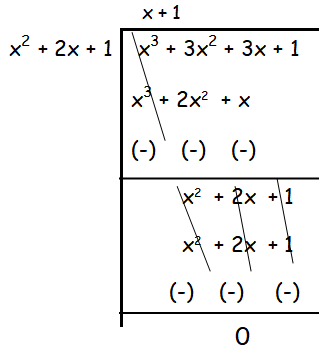
Hence G.C.D of the given polynomials is x² + 2x + 1.

Question 3 :

Reduce the given Rational expressions to its lowest form

(i)  (x^3a - 8)/(x^2a + 2x^a + 4)

Solution  :

(x^3a - 8)/(x^2a + 2x^a + 4)

  =  ((x^a)³ - 2³)/((x^a)² + 2x^a + 2²)

  =  ((x^a - 2)((x^a)² + 2x^a + 2²)/((x^a)² + 2x^a + 2²)

  =  (x^a - 2)

(ii)  (10x³ - 25x² + 4x - 10)/(-4 - 10x²)

Solution :

(10x³ - 25x² + 4x - 10)/(-4 - 10x²)

  =  -(10x³ - 25x² + 4x - 10)/(10x² + 4)

  =  -(10x³ - 25x² + 4x - 10)/2(5x² + 2)

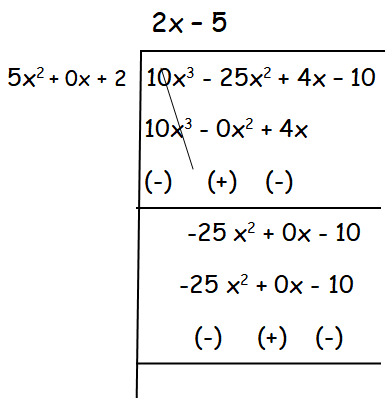
=  -(2x - 5)/2

=  -x + (5/2)

Question 4 :

Simplify 

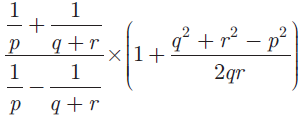
Solution :

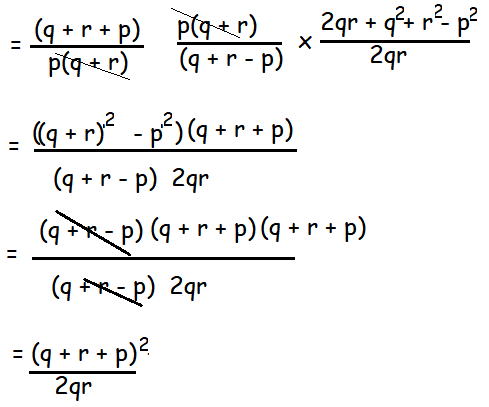
Question 5 :

Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone?

Solution :

Let x, y and z be the quantity of works finished by Arul, Ravi and Ram respectively.

y = 2x  and z = 3x

1 hour work by Arul  =  1/x

1 hour work by Ravi  =  1/y

1 hour work by Ram  =  1/z

1/x + (1/2x) + (1/3x)  =  1/6

(6 + 3 + 2)/6x  =  1/6

11/6x  =  1/6

x  =  11 hours (No of hours taken by Arul)

2x  =  2(11)  =  22 hours (taken by Ravi)

3x  =  3(11)  =  33 hours (taken by Ram)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.