FINDING MEDIAN FOR GROUPED DATA

Median is the value which occupies the middle position when all the observations are arranged in an ascending or descending order. It is a positional average.

(i) Construct the cumulative frequency distribution.

(ii)  Find (N/2)^th term

(iii) The class that contains the cumulative frequency N/2 is called the median class. 

(iv) Find the median by using the formula:

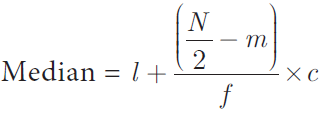
Where l = Lower limit of the median class,

f = Frequency of the median class

c = Width of the median class,

N = The total frequency (∑f)

m = cumulative frequency of the class preceeding the median class

Example 1 :

The following are the marks scored by the students in the Summative Assessment exam. 

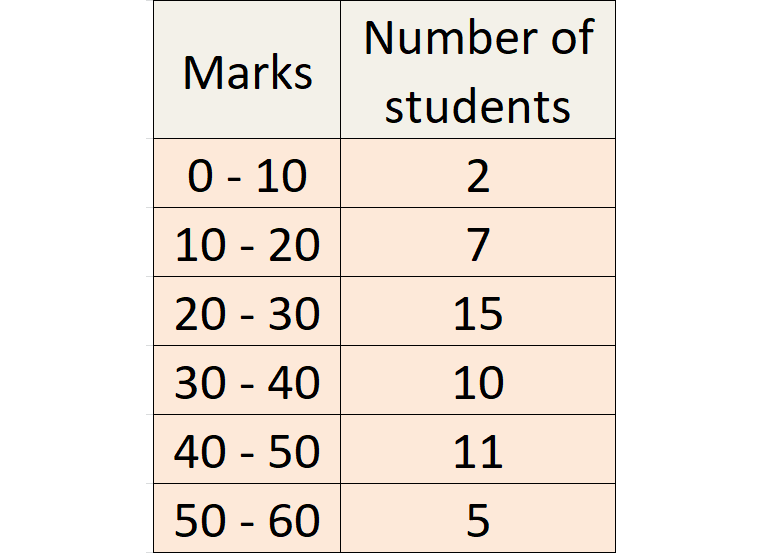
Calculate the median. 

Solution :

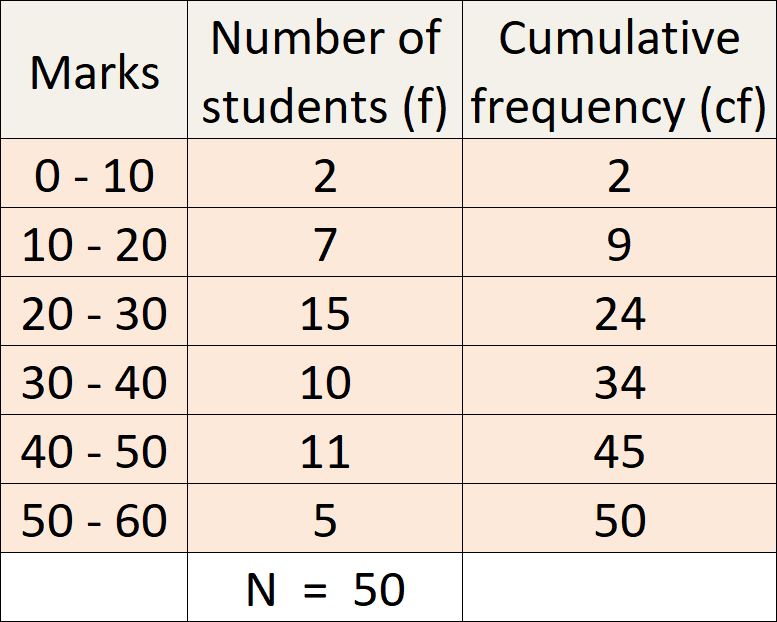
Median class  =  (N/2)^th value

=  (50/2)^th value

=  25^th value

Median class  =  20 - 30

l = 20, N//2  =  25, m = 9, f = 15 and c = 10

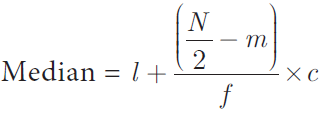
Substitute.

Median  =  20 + ([25 - 9]/15) x 10

=  20 + (16/15) x 10

=  20 + 10.6 

=  30.6

≈  31

Example 2 :

The following table gives the weekly expenditure of 200 families. Find the median of the weekly expenditure.

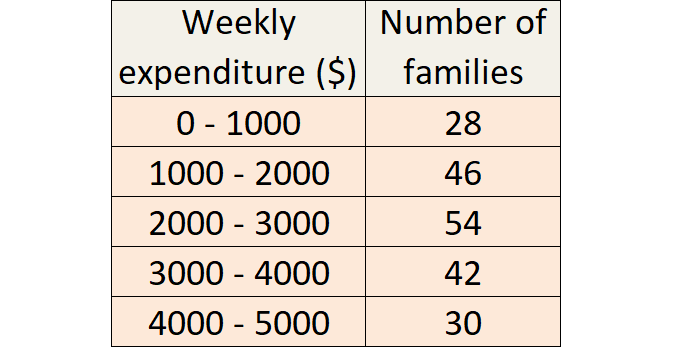
Solution : 

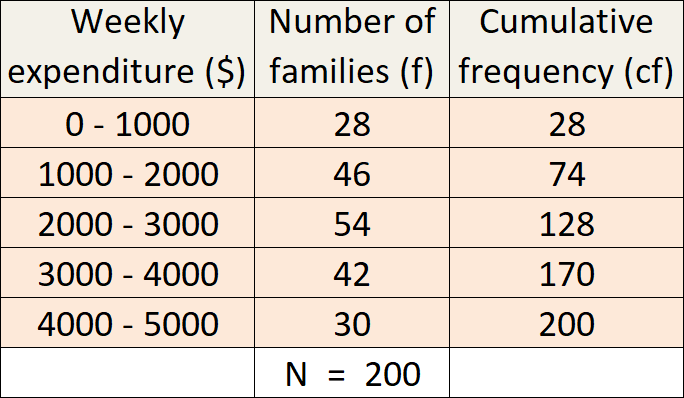
Median class  =  (N/2)^th value

=  (200/2)^th value

=  100^th value

Median class  =  2000 - 3000

l = 2000, N//2  =  100, m = 74, f = 54 and c = 1000

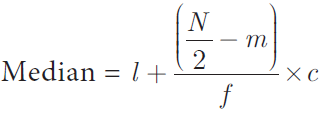
Substitute.

Median  =  2000 + ([100 - 74]/54) x 1000

=  2000 + (26/54) x 1000

=  2000 + 481.5

=  2481.5

Example 3 :

The Median of the following data is 24. Find the value of x.

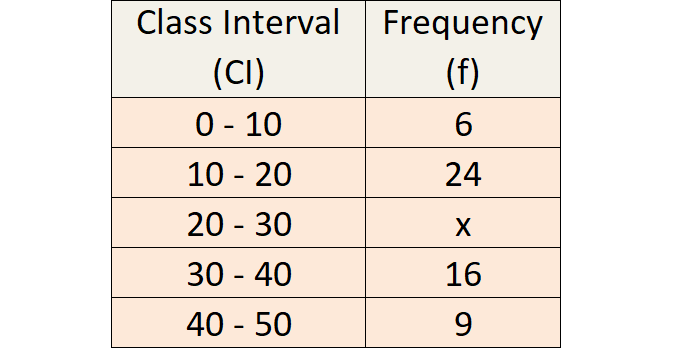
Solution : 

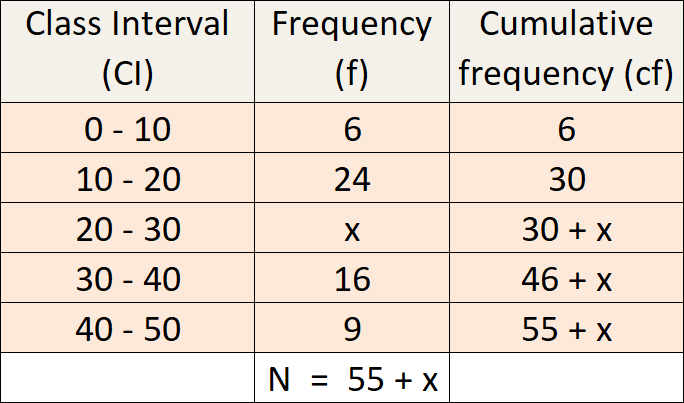
Since the median is 24 and median class is 20 – 30.

l = 20 N = 55 + x, m = 30, c = 10, f = x

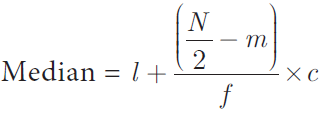
Substitute. 

24  =  20 + {[(55 + x)/2 - 30] / x} ⋅ 10

4  =  {[(x - 5)/2] / x} ⋅ 10

4  =  {(x - 5) / 2x} ⋅ 10

4  =  {(x - 5) / x} ⋅ 5

4  =  (5x - 25) / x

4x  =  5x - 25

25  =  5x - 4x

25  =  x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.