FINDING THE EQUATION OF A CIRCLE IN GENERAL FORM

Here we are going to see some example problems to know how to find equation of a circle in general form.

Standard equation of a circle with centre (0, 0) and radius r :

x² + y²  =  r²

Equation of a circle with centre (h, k) and radius r :

(x - h)² + (y - k)²  =  r²

General form of the equation of a circle : 

x² + y² + 2gx + 2fy + c  =  0

Example 1 :

Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form.

Solution :

Equation of a circle with centre (h, k) and radius r :

(x - h)² + (y - k)²  =  r²

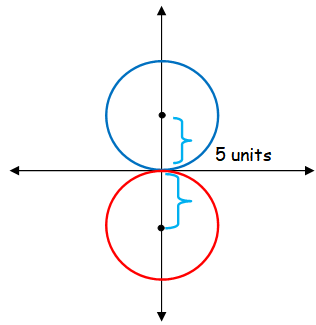
The center lies on y axis. The center point will be at (0, 5) and (0, -5).

So, the required equations are 

x² + y² - 10y  =  0 and x² + y² + 10y  =  0

Example 2 :

Find the equation of the circle with centre (2, -1) and passing through the point (3, 6) in general form.

Solution :

Equation of a circle with centre (h, k) and radius r :

(x - h)² + (y - k)²  =  r²

Centre (h, k)  ==>  (2, -1).

(x - 2)² + (y + 1)²  =  r² -----(1)

The given circle is passing through the point (3, 6). 

Then, substitute 3 for x and 6 for y. 

(3 - 2)² + (6 + 1)²  =  r²

1² + 7²  =  r²

1 + 49  =  r²

50  =  r²

Then, 

 (1)-----> (x - 2)² + (y + 1)²  =  50

x² - 2(x)(2) + 2² + y² + 2(y)(1) + 1²  =  50

x² - 4x + 4 + y² + 2y + 1  =  50

x² + y² - 4x + 2y + 5  =  50

Subtract 50 from each side. 

x² + y² - 4x + 2y - 45  =  0

Example 3 :

Find the equation of circles that touch both the axes and pass through (-4, -2) in general form

Solution :

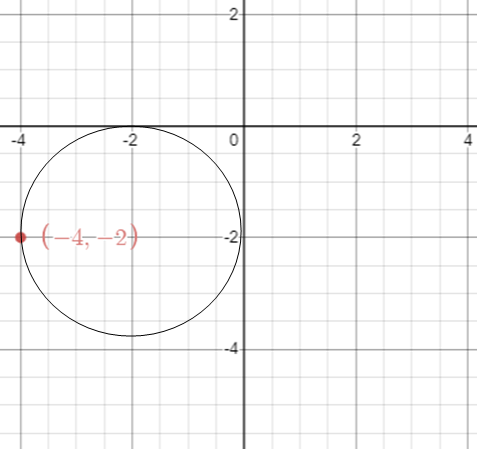
The center point will be at (-r, -r)

By applying the point passes through the circle and center, we get

(x - h)² + (y - k)²  =  r²  

(-4 + r)² + (-2 + r)²  =  r²  

16 + r² - 8r + 4 - 4r + r² - r²  =  0

20 + r² - 12r  =  0

r² - 12r + 20  =  0

(r - 10) (r - 2)  =  0

r  =  10 and r  =  2

Equation of a circle center is at (-10, -10) and radius is 10.

(x + 10)² + (y + 10)²  =  10²  

x² + 20x + 100 + y² + 20y + 100 - 100  =   0

x² + 20x + y² + 20y + 100  =  0

x² + y² + 20x + 20y + 100  =  0

Equation of a circle center is at (-2, -2) and radius is 2.

(x + 2)² + (y + 2)²  =  2²  

x² + 4x + 4 + y² + 4y + 4 - 4  =   0

x² + 4x + y² + 4y + 4  =  0

x² + y² + 4x + 4y + 4  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.