FINDING THE MISSING LENGTH OF A RIGHT TRIANGLE

If the lengths of two sides of a right triangle are given, we can use Pythagorean Theorem to find the length of the missing side.

Pythagorean Theorem : 

Square of the hypotenuse of a right triangle is equal to sum of the squares of other two sides.

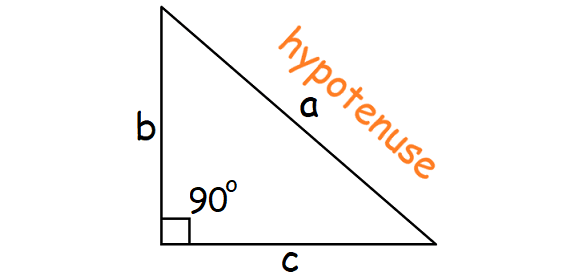
a² = b² + c²

If you know the values of any two variables, you can solve for the third variable using the above equation.

Note :

Hypotenuse is the longest side of a right triangle and it is always opposite to the right angle.

Example 1 :

In the right triangle shown below, find the value of 'a'.

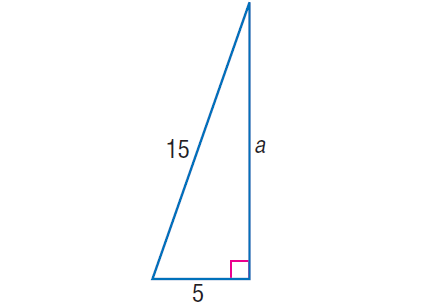
Solution :

In the right triangle above, by Pythagorean Theorem,

15²  =  5² + a²

225  =  25 + a²

Subtract 25 from both sides.

200 = a²

Take square root on both sides.

√200 = √a²

√(2 x 10 x 10) = a

10√2 = a

Example 2 :

In the right triangle shown below, find the value of 'c'.

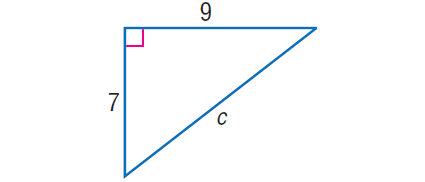
Solution :

In the right triangle above, by Pythagorean Theorem,

c² = 7² + 9²

c² = 49 + 81

c² = 130

Take square root on both sides.

√c² = √130

c = √130

Example 3 :

In the right triangle shown below, find the value of 'c'.

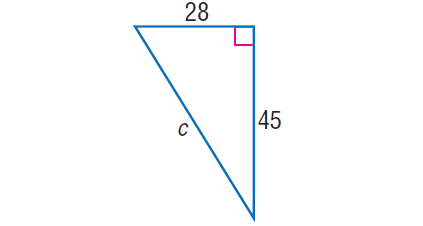
Solution :

In the right triangle above, by Pythagorean Theorem,

c² = 28² + 45²

c² = 784 + 2025

c² = 2809

Take square root on both sides.

√c = √2809

c = 53

Example 4 :

In the right triangle shown below, find the value of 'b'.

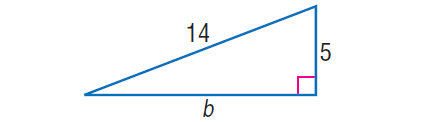
Solution :

In the right triangle above, by Pythagorean Theorem,

14² = 5² + b²

196 = 25 + b²

Subtract 25 from both sides.

171 = b²

√171 = √b²

√171 = b

Example 5 :

In the right triangle shown below, find the value of 'a'.

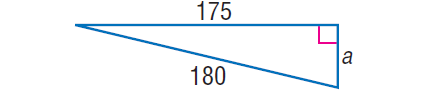
Solution :

In the right triangle above, by Pythagorean Theorem,

180² = a² + 175²

32400 = a² + 30625

Subtract 30625 from both sides.

1775 = a²

√1775 = √a²

√(5 x 5 x 71) = a

5√71 = a

Example 6 :

In the right triangle shown below, find the value of 'b'.

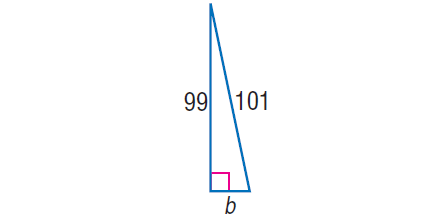
Solution :

In the right triangle above, by Pythagorean Theorem,

101² = b² + 99²

10201 = b² + 9801

Subtract 9801 from both sides.

400 = b²

√400 = √b²

20 = b

Example 7 :

Let a, b and c be the lengths of the sides of a right triangle. If a = 16, b = 63 and c is the length of hypotenuse, then find the value of c.

Solution :

By Pythagorean Theorem,

c² = a² + b²

Substitute a = 16 and b = 63.

c² = 16² + 63²

c² = 256 + 3969

c² = 4225

Take square root on both sides.

√c² = √4225

c = 65

Example 8 :

Let a, b and c be the lengths of the sides of a right triangle. If a = 16, c = 34 and c is the length of hypotenuse, then find the value of b.

Solution :

By Pythagorean Theorem,

c² = a² + b²

Substitute a = 16 and c = 34.

34² = 16² + b²

1156 = 256 + b²

Subtract 256 from both sides.

900 = b²

Take square root on both sides.

√900 = √b²

30 = b

Example 9 :

Let a, b and c be the lengths of the sides of a right triangle. If b = √112, c = 3 and a is the length of hypotenuse, then find the value of a.

Solution :

By Pythagorean Theorem,

a² = b² + c²

Substitute b = √112 and c = 3.

a² = (√112)² + 3²

a² = 112 + 9

a² = 121

Take square root on both sides.

√a² = √121

a = 11

Example 10 :

Let a, b and c be the lengths of the sides of a right triangle. If a = 7y, c = 3y and a is the length of hypotenuse, then find the value of b in terms of y.

Solution :

a² = b² + c²

(7y)² = b² + (3y)²

49y² = b² + 9y²

Subtract 9y² from both sides.

40y² = a²

Take square root on both sides.

√(40y²) = √a²

2y√10 = a

Example 11 :

The bottom of a ladder must be placed 3 feet from a wall. The ladder is 12 feet long.  How far above the ground does the ladder touch the wall? 

Solution :

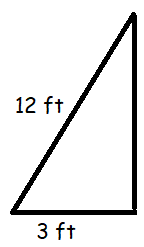
Let x be the distance from ground to tip of the wall it touches.

Using Pythagorean theorem,

12² = 3² + x²

144 = 9 + x²

x² = 144 - 9

x² = 135

x = √135

x = √(5 x 3 x 3 x 3)

= 3√15 ft

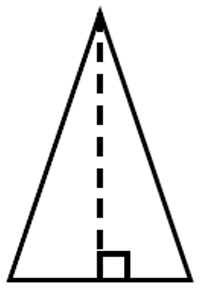
Example 12 :

An isosceles triangle has congruent sides of 20 cm.  The base is 10 cm.  What is the area of the triangle? 

Solution :

Half of the base = 5 cm, side length = 20 cm

Let x be the height of the triangle.

20² = 5² + x²

400 = 25 + x²

x² = 400 - 25

x² = 375

x = √375

x = √(5 x 5 x 5 x 3)

= 5√15 cm

Example 13 :

The area of a square is 81 cm².  Find the length of diagonal.

Solution :

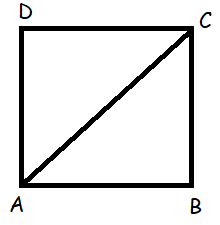
Let x be the side length of square.

Area of square = 81

a² = 81

a² = 9²

a = 9

Let d be the length of diagonal. Then,

d² = a² + a²

d² = 9² + 9²

= 81 + 81

= 162

d = √162

d = √(2 x 9 x 9)

d = 9√2

So, the length of the diagonal is 9√2 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.