FINDING TRIG FUNCTIONS IF THE TERMINAL SIDE PASSES THROUGH GIVEN POINT

Question :

Determine the exact values of sin θ, cos θ and tan θ if the terminal arm of an angle in standard position passes through the given point.

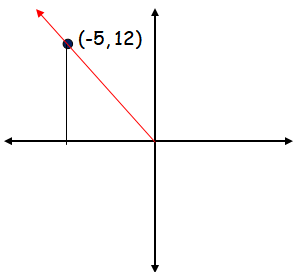
a) P (-5, 12)

Solution :

Horizontal distance  =  5, vertical distance  =  12

Length of hypotenuse side  =  √12² + 5²

  =  √(144 + 25)

  =  √169   

  =  13

Since the terminal arm lies in second quadrant, we have to use positive sign for sin and cosec.

sin θ  =  12/13, cos θ  =  -5/13 and tan θ  =  -12/5

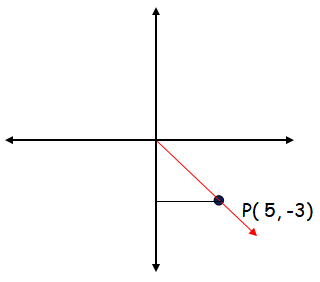
(b) P(5, -3)

Solution :

Horizontal distance  =  5, vertical distance  =  3

Length of hypotenuse side  =  √5² + 3²

  =  √(25 + 9)

  =  √34   

Since the terminal arm lies in fourth quadrant, we have to use positive sign for cos and sec.

sin θ  =  -5/√34, cos θ  =  3/√34 tan θ  =  -5/3

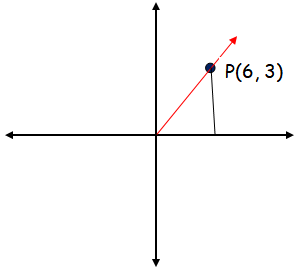
(c) P(6, 3)

Solution :

Horizontal distance  =  6, vertical distance  =  3

Length of hypotenuse side  =  √6² + 3²

  =  √(36 + 9)

  =  √45  =  3√5

Since the terminal arm lies in first quadrant, we have to use positive sign for all trigonometric ratios.

sin θ  =  3/3√5  =  1/√5

cos θ  =  6/3√5  =  2/√5

 tan θ  =  1/2

d) P(-24, -10)

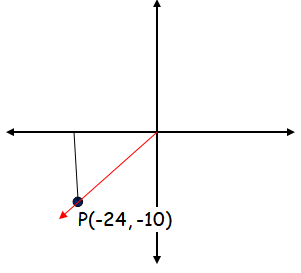
Solution :

Horizontal distance  =  24, vertical distance  =  10

Length of hypotenuse side  =  √24² + 10²

  =  √(576 + 100)

  =  √676  =  26

Since the terminal arm lies in third quadrant, we have to use positive sign for tan and cot only.

sin θ  =  -10/26  =  -5/13

cos θ  =  -24/26  =  -12/13

 tan θ  =  5/12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.