FINDING UNKNOWN ANGLES IN QUADRILATERALS WORKSHEET

Problem 1 : 

In the diagram shown below, find m∠A. 

Solution

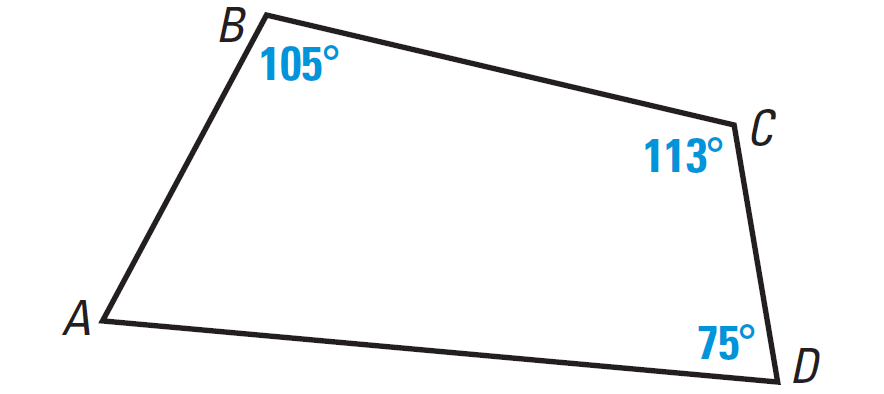
Problem 2 : 

In the diagram shown below, find the value of x. 

Solution

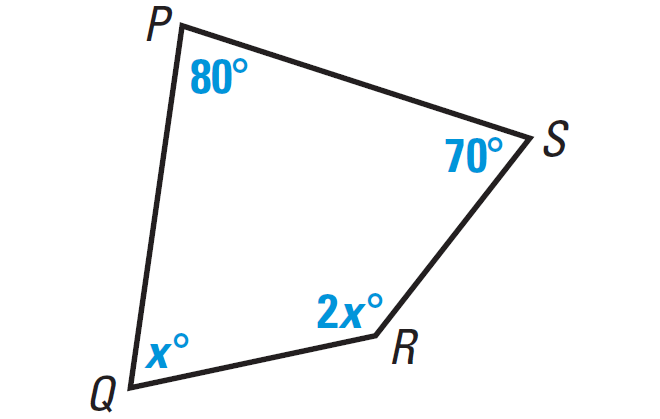
Problem 3 : 

In the diagram shown below, find m∠A. 

Solution

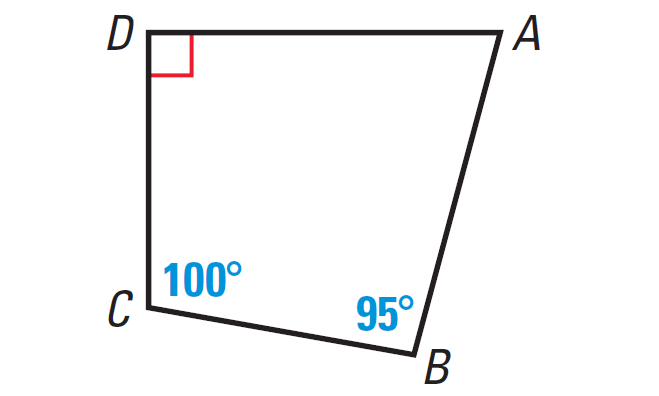
Problem 4 : 

In the diagram shown below, find the value of x. 

Solution

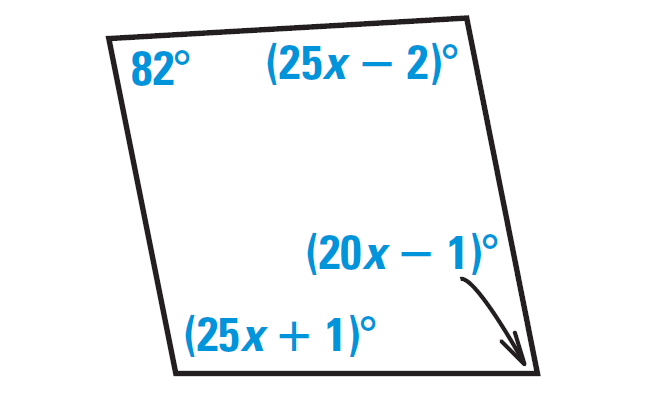
Problem 5 : 

In the diagram shown below, find the value of x.

Solution

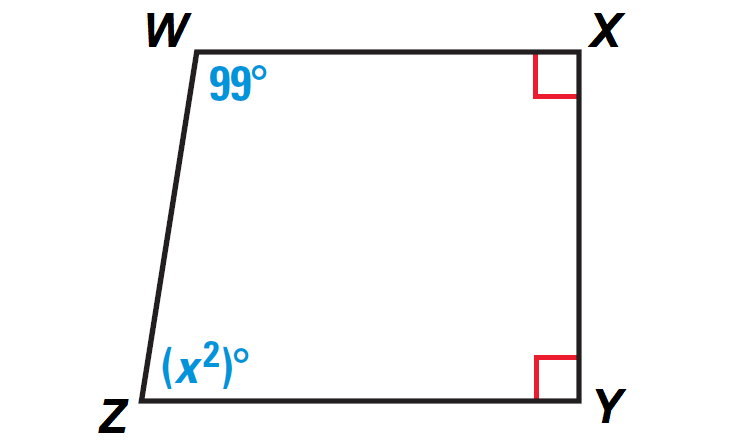
Problem 6 : 

In the diagram shown below, find the value of x. 

Solution

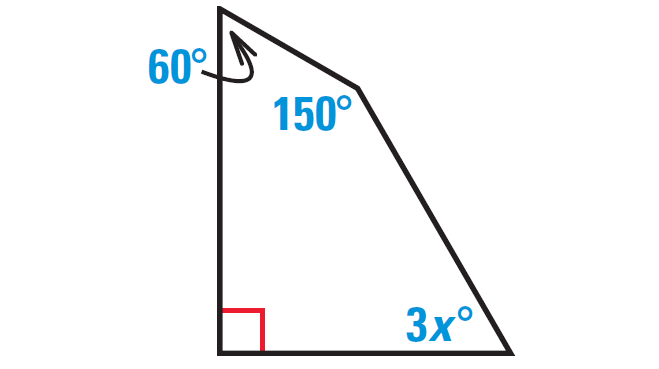
Problem 7 : 

In the diagram shown below, find the value of x.

Solution

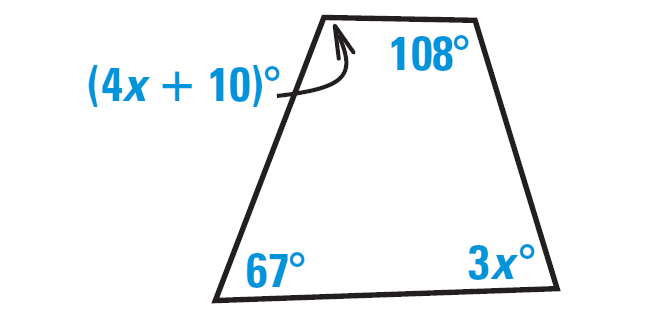
Problem 8 : 

In the diagram shown below, find the values of x and y. 

Solution

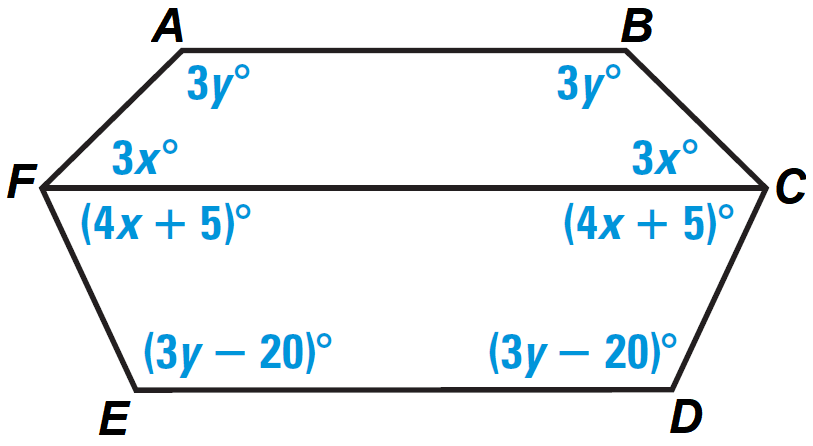
Problem 9 : 

In the diagram shown below, find the value of x.

Solution

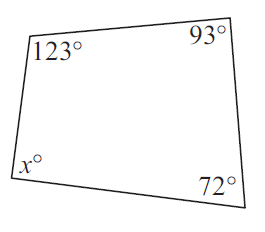
Problem 10 : 

In the diagram shown below, find the value of a.

Solution

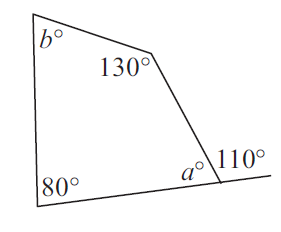
Problem 11 : 

In the diagram shown below, find the value of a.

Solution

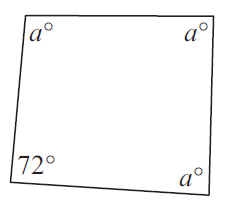
Problem 12 : 

In the diagram shown below, find the values of a and b.

Solution

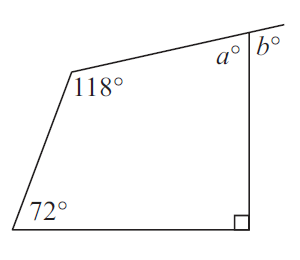
Problem 13 : 

In the diagram shown below, find the values of a and b.

Solution

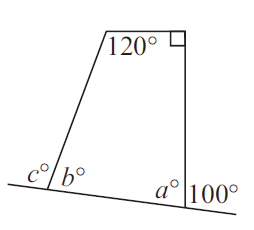
Problem 14 : 

In the diagram shown below, find the value of a.

Solution

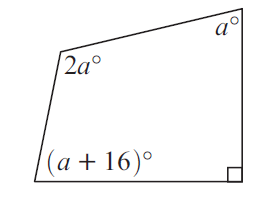
Problem 15 : 

In the diagram shown below, find the values of a, b, c and d.

Solution

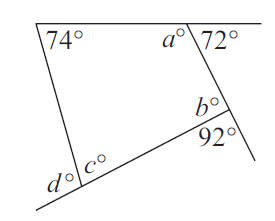
Problem 16 :

Two adjacent sides AB and BC of a parallelogram ABCD are in the ratio 5 : 3. If the perimeter is 200 cm, what is the length of AB and BC ?

(a) 25 cm & 50 cm     (b) 40 cm & 37.5 cm

(c) 62.5 cm & 37.5 cm     (d) 60 cm & 62.5 cm

Solution

Problem 17 :

One angle of a parallelogram is 60°. Find its opposite angle and the adjacent angle

Solution

Problem 18 :

ABCD is a trapezium with AB || DC. If ∠A = 50°, then find ∠D.

Solution

Problem 19 :

Four angles of quadrilaterals are in the ratio 3 : 4 : 5 : 6. Find its angles.

Solution

Problem 20 :

ABCD is a rhombus with ∠DAB = 56, determine ∠DBC

Solution

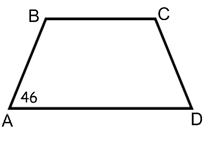
Problem 21 :

In the following diagram of isosceles trapezoid ∠A = 46 . Find the measure of all of the remaining angles.

Solution

Problem 22 :

Four angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. Find its angles.

Solution

Problem 23 :

The adjacent angels of a parallelogram are (3x - 4)° and (3x + 10)°. Find the angles of a parallelogram.

Solution

Problem 24 :

Three angles of a quadrilateral are in the ratio 4 : 6 : 3. If the fourth angle is 100°, find the three angles of a quadrilateral.

Solution

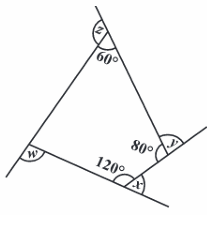
Problem 25 :

Find x + y + z + w

Solution

Problem 26 :

Find the angle x.

Solution

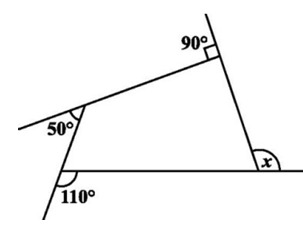
Problem 27 :

Two adjacent angles of a parallelogram are as 2 : 3. Find the measure of each of its angles.

Solution

Problem 28 :

The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle is 80°   . Find the obtuse angle.

Solution

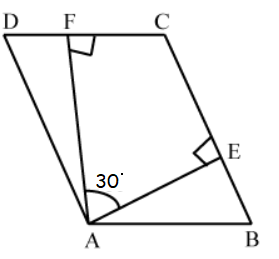
Problem 29 :

In a figure given below, ABCD is a parallelogram, what is the value of x ?

Solution

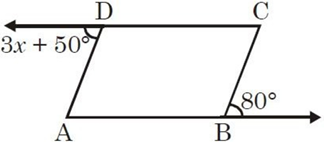
Problem 30 :

Show that the bisectors of angles of a parallelogram form a rectangle .

Solution

Problem 31 :

If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram.

Solution

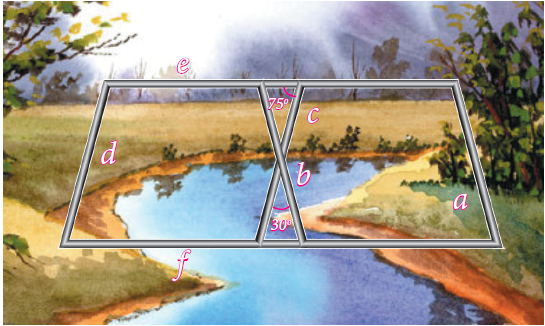
Problem 32 :

Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b , c || d , e || f , find the marked angles between

(i) b and c

(ii) d and e

(iii d and f

(iv) c and f

Solution

(1)  m∠A  =  67°

(2)  x  =  70

(3)  m∠A  =  75°

(4)  x  =  4

(5)  x  =  9

(6)  x  =  20

(7)  x  =  25

(8)  x  =  15 and y  =  45

(9)  x  =  72

(10)  a  =  70 and <b  =  80

(11)  <a  =  93

(12)  <a  =  80 and <b  =  100

(13)  <a  =  80, <b  =  70 and <c  =  110.

(14)  a  =  61

(15)  <a  =  106, <b  =  88, <c  =  92 and <d  =  88.

16)  The side lengths are 62.5 cm and 37.5 cm. Option c is correct.

17)  x = 120

18)  ∠D = 130

19)  So, the angle measures are 60, 80, 100 and 120.

20)  ∠DBC = 124

21) ∠B and ∠C = 134

22)  So, the required angles are 60°, 80°, 100° and 120°

23)  So, the required angels are 84° and 97°

24)  So, the required angles are 80°, 120°, 60° and 100°

25)  x + y + z + w = 380°

26)  So, the required angles are 72, 72, 108 and 108.

27)  So, the required obtuse angle is 150 degree

28)  So, the value of x is 10.

31)  

(i)  Angle between b and c is 30.

(ii)  Angle  between d and e :

75 + angle between d and e  =  180

Angle between d and e  =  180 - 75

  =  105

(iii)  Angle between d and f :

Angle between d and is also 75.

(iv)  Angle between c and f :

Angle between c and f is 105.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.