FINDING THE X INTERCEPTS OF A QUADRATIC FUNCTION

Quadratic Function with One X-Intercept

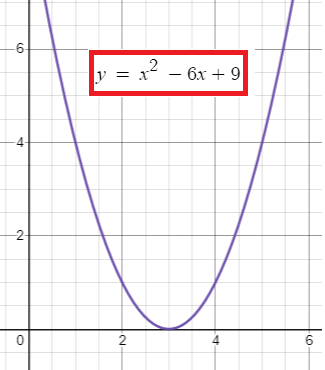
Quadratic Function with Two X-Intercepts

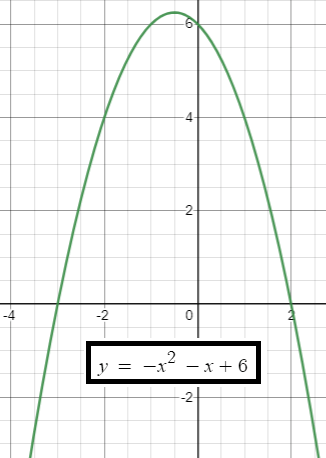
Find the x intercept(s) of the quadratic functions :

Example 1 :

y = x²- 6x + 9

Solution :

y = x²  - 6x + 9

Substitute y = 0 to to find x-intercepts.

x² - 6x + 9 = 0

In the quadratic equation above, the coefficient of x² is 1. So, get two factors of the constant term '+9' such that the sum of the two factors is equal to the coefficient of x, that is '-6'.

Then the two factors of '+9' are '-3' and '-3'.

Now, split the middle term -6x using the two factors -3 and -3.

x² - 6x + 9 = 0

x² - 3x - 3x + 9 = 0

x(x - 3) - 3(x - 3) = 0

(x - 3)(x - 3) = 0

(x - 3)² = 0

Taking square root on both sides,

x - 3 = 0

x = 3

The given quadratic expression has only one x-intercept and it is 3.

Example 2 :

y = x² - 3x + 2

Solution :

y = x² - 3x + 2

Substitute y = 0 to to find x-intercepts.

x² - 3x + 2 = 0

In the quadratic equation above, the coefficient of x² is 1. So, get two factors of the constant term '+2' such that the sum of the two factors is equal to the coefficient of x, that is '-3'.

Then the two factors of '+2' are '-1' and '-2'.

Now, split the middle term -3x using the two factors -1 and -2.

x² - 3x + 2 = 0

x² - 1x - 2x + 2 = 0

x(x - 1) - 2(x - 1) = 0

(x - 1)(x - 2) = 0

x - 1 = 0  or  x - 2 = 0

x = 1  or  x = 2

The given quadratic expression has two x-intercepts and they are 1 and 2.

Example 3 :

y = -9x² + 4

Solution :

Substitute y = 0 to to find x-intercepts.

 -9x² + 4 = 0

Multiply both sides by -1.

9x² - 4 = 0

3²x² - 4 = 0

(3x)² - 2² = 0

Using the identity a² - b² = (a + b)(a - b),

(3x + 2)(3x - 2) = 0

3x + 2 = 0  or  3x - 2 = 0

x = -2/3  or  x = 2/3

The given quadratic expression has two x-intercepts and they are -2/3 and 2/3.

Example 4 :

y = 3x² - x - 2

Solution :

Substitute y = 0 to to find x-intercepts.

 3x² - x - 2 = 0

In the quadratic expression above, the coefficient of x² is 3.

Multiply the coefficient of x² and the constant term -2.

3x(-2) = -6

Now, get two factors of '-6' such that the sum of the two factors is equal to the coefficient of x, that is '-1'.

Then the two factors of '-6' are '+2' and '-3'.

Now, split the middle term -x using the two factors +2 and -3.

 3x² - x - 2 = 0

3x² + 2x - 3x - 2 = 0

x(3x + 2) - 1(3x + 2) = 0

(3x + 2)(x - 1) = 0

3x + 2 = 0  or  x - 1 = 0

x = -2/3  and  x = 1

The given quadratic function has two x-intercept and they are -2/3 and 1.

Example 5 :

y = -(x - 1)(x - 3)

Solution :

y = -(x - 1)(x - 3)

Substitute y = 0 to to find x-intercepts.

-(x - 1)(x - 3) = 0

Multiply both sides of the equation by -1.

(x - 1)(x - 3) = 0

x - 1 = 0  or  x - 3 = 0

x = 1  or  x = 3

The given quadratic function has two x-intercept and they are 1 and 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.