FORM THE DIFFERENTIAL EQUATION BY ELIMINATING ARBITRARY CONSTANT

Form a differential equations by eliminating arbitrary constants given in brackets against each.

(1)  y²  =  4ax       {a}

(2)  y  =  ax²+bx+c       {a, b}

(3) x y = c²       {c}

(4)  (x²/a²) + (y²/b²)  =  1     {a, b}

(5)  y  =  A e^2x + Be^-5x         {A, B}

(6)  y  =  e^3x (C cos2x + D sin2x)    {C, D}

(7)  y  =  e^mx         {m}

(8)  y  =  Ae^2x cos (3x + B)      {A, B}

Problem 1 :

y²  =  4ax       {a}

Solution  :

Number of arbitrary constant is 1, so we may  differentiate the equation once to find the differential equation.

2y(dy/dx)  =  4a(1)

2y(dy/dx)  =  4a

dy/dx  =  4a/2y

dy/dx  =  2a/y  ---- (1)

By finding the value of y from equation (1), we get

y²  =  4ax

a  =  y²/4x

now we are going to apply the value of a in the first equation

dy/dx  =  2(y²/4x)/y

dy/dx  =  2y²/4xy

y'  =  y/2x

2xy'  =  y

y  =  2xy'

Therefore the required equation is y  =  2xy'.

Problem 2 :

y  =  ax²+bx+c       {a, b}

Solution :

Number of arbitrary constants is 2, so the order of required differential equation is 2.

y  =  ax²+bx+c   --- (1)

differentiate with respect to x

dy/dx  =  a (2x)+b(1)+0

dy/dx  =  2ax+b

again differentiate the above equation with respect to x

d²y/dx²  =  2a(1)+0

d²y/dx²  =  2a 

y'  =  2ax+b     --- (2)

y''  =  2a    --- (3)

By applying the value of 2a in (2), we get

y'  =  y''x+b

b  =  y'-y''x

a  =  y''/2

By applying the values of a and b in (1), we get

y  =  ax²+bx+c

y  =  (y''/2)x² + (y'-y'' x)x + c

y  =  (y''x  /2) + y'x - y''x²+ c

y  =  (y''x² + 2 y' x - 2 y'' x² + 2 c)/2

2y  =  2y'x-y''x²+2c

x²y''-2xy'+2y-2c  =  0

Therefore the required differential equation is

x²y''-2xy'+2y-2c  =  0

Problem 3 :

xy  =  c²       {c}

Solution :

Number of arbitrary constants is 1, so we can differentiate the equation once to get the required differential equation.

xy  =  c²

x (dy/dx)+y(1)  =  0

xy'+y  =  0

Therefore the required equation is

xy'+y  =  0

Problem 4 :

(x²/a²) + (y²/b²)  =  1     {a , b}

Solution :

(x²/a²) + (y²/b²)  =  1

(x²b² + y²a²)/a²b²  =  1

x²b² + y²a²  =  a²b²

Number of arbitrary constants is 2, so to find the differential equation, we can differentiate the equation twice.

Differentiate the given equation with respect to x

2xb²+2yy'a²  =  0

divide the whole equation by 2

xb²+yy'a²  =  0  ------ (1)

Again differentiate the given equation with respect to x

we are going to differentiate y y' using product rule

u = y      v = y'

u' = y'     v' = y''

Formula for product rule :

d (u v)  =  u v' + v u'

=  yy''+y'(y')

=  y y''+(y')²

(1) b² + [y y''+(y')²] a²  =  0

b² + [y y''+(y')²] a²  =  0 ----- (2)

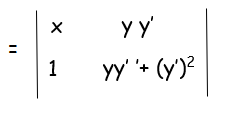
x(yy''+(y')²) -1(yy')  =  0

xy''+xyy' - yy'  =  0

Problem 5 :

y  =  A e^2x + Be^-5x         {A , B}

Solution :

y  =  A e^2x + Be^-5x   -----(1)

y' =  2Ae^2x -5 Be^-5x  -----(2)

y'' = 4 Ae^2x +25 Be^-5x     -----(3)

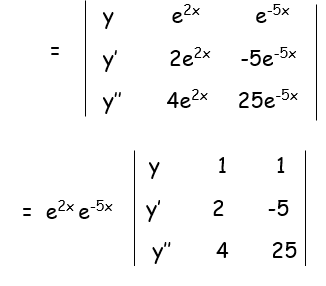
=  e^-3x[y(50+20)-1(25y'+5y'') + 1(4y'-2y'')]

=  e^-3x[70y-25y'-5y'' + 4y'-2y'']

=  e^-3x[70y-21y'-7y'']

70y-21y'-7y''  =  0

Divide the equation by (-7), we get

y''+3y'-10y  =  0

So, the required differential equation is

y''+3y'-10y  =  0

Problem 6 :

y  =  e^3x (C cos2x + D sin2x)    {C, D}

Solution :

y  =  e^3x (C cos2x + D sin2x)

ye^-3x  =  (C cos2x + D sin2x)  ---(1)

Differentiating with respect to x, we get

-3ye^-3x+e^-3xy'  =  -2C sin 2x + 2D cos 2x

e^-3x(y'-3y)  =  -2C sin 2x + 2D cos 2x

Again differentiating with respect to x, we get

e^-3x(y''-3y')+(y'-3y)(-3e^-3x)  =  -4C cos 2x - 4D sin 2x

e^-3x[(y''-3y')-3(y'-3y)]  =  -4(C cos 2x + D sin 2x)

(y''-6y'-9y)  =  -4e^3x(C cos 2x + D sin 2x)

(y''-6y'-9y)  =  -4y

y''-6y'-9y+4y  =  0

y''-6y'-5y  =  0

So, the required differential equation is 

y''-6y'-5y  =  0.

Problem 7 :

y  =  e^mx         {m}

Solution :

y  =  e^mx

y'  =  me^mx

y'  =  3y

y'-3y  =  0

So, the required differential equation is 

y'-3y  =  0

Problem 8 :

y  =  Ae^2x cos (3x + B)      {A, B}

Solution :

y  =  Ae^2x cos (3x+B)

ye^-2x  =  A cos (3x+B)  ------(1)

-2ye^-2x + e^-2x y'  =  -3A sin(3x+B)

e^-2x(-2y+y')  =  -3A sin(3x+B)  ------(2)

e^-2x(-2y+y')  =  -9A cos(3x+B) 

(-2y+y')  =  -9Ae^2x cos(3x+B) ------(3)

-2y+y'  =  -9y

y'+9y-2y  =  0

y'+7y  =  0

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.