FUNCTION NOTATION INPUT AND OUTPUT WORKSHEET

Problem 1 :

If f(x) = 5x - 7, evaluate f(x) in each case for the given value of x.

(i) f(2)

(ii) f(0)

(iii) f(-1)

(iv) f(½)

Problem 2 :

If g(y) = -5y + 2, evaluate g(y) in each case for the given values of y.

(i) g(0)

(ii) g(5)

(iii) g(-4)

(iv) g(⁻¹⁄₄)

Problem 3 :

If h(z) = 5 - (½)z, evaluate h(z) in each case for the given value of z.

(i) h(-2)

(ii) h(4)

(iii) h(0)

(iv) h(0.5)

Problem 4 :

If f(x) = 3x + 2, find the value of x in each case for the given value of f(x).

(i) f(x) = 8

(ii) f(x) = -7

(iii) f(x) = 0.5

(iv) f(x) = ⁻¹⁄₄

Problem 5 :

If g(y) = -5y + 1, find the value of y in each case for the given value of g(y).

(i) g(y) = 26

(ii) g(y) = 0

(iii) g(y) = -14

(iv) g(y) = ⁻⁵⁄₂

Problem 6 :

If h(z) = (⁻¹⁄₂)z + 7, find the value of z in each case for the given value of h(z).

(i) h(z) = 7

(ii) h(z) = -2

(iii) h(z) = 0

(iv) h(z) = ¹⁄₄

Problem 7 :

g(y) = 7y - a

In the function above, a is a constant and g(5) = 17. What is the value of g(-2)?

Problem 8 :

If h(1 - z) = 3z - 2, find the value of h(-1).

Problem 9 :

An online film renting service charges a one time fee of $35 for 1 year subscription and $7 for each film rented in that year. Find the function which models the total charge for x number of films in a year. And also, find the total charge for 15 films rented in a year.

Problem 10 :

A tank contains 27.5 gallons of water now and water is being pumped into the tank at a rate of 2 gallons per minute. Write the function that models the amount of water in the tank in x minutes from now. And also, find the amount of water in the tank 20 minutes from now.

Answers

1. Answer :

2. Answer :

3. Answer :

4. Answer :

5. Answer :

6. Answer :

7. Answer :

To find the value of g(-2), first we have to find the value of the constant a in the given function g(y) = 7y - a.

g(y) = 7y - a

g(5) = 7(5) - a

g(5) = 35 - a ----(1)

It is given that

g(5) = 17 ----(2)

From (1) and (2),

35 - a = 17

-a = -18

a = 18

Now, the given function is

g(y) = 7y - 18

Substitute y = -2.

g(-2) = 7(-2) - 18

= -14 - 18

= -32

8. Answer :

The given function is not in the form h(z). So, we can not substitute z = -1 in h(1 - z) First, we have to change the given function to the regular form h(x). Then, we have to substitute x = -1 to evaluate h(-1).

h(1 - z) = 3z - 2 ----(1)

Let x = 1 - z.

Solve for z in terms of x.

x = 1 - z

x + z = 1

z = 1 - x

Substitute x for '1 - z' and '1 - x' for z in (1).

h(x) = 3(1 - x) - 2

h(x) = 3 - 3x - 2

h(x) = -3x + 1

Substitute x = -1.

h(-1) = -3(-1) + 1

h(-1) = 3 + 1

h(-1) = 4

9. Answer :

It is given that that charge for each film rented is $12.

1 film ----> $7

x(1 film) ----> x($7)

x films = 7x

Total charge for 1 year (including onetime fee) :

= 7x + 50

Therefore, the function which models the total charge for 1 year :

T(x) = 7x + 50

To find the total charge for 15 films, substitute x = 15 into the above function.

T(15) = 7(15) + 35

= 105 + 35

= 140

The total charge for 15 films rented in a year is $140.

10. Answer :

It is given that water is being pumped into the tank at a rate 2 gallons per minute.

1 minute ----> 2 gallons

x(1 minute) ----> x(2 gallons)

x minutes ----> 2x gallons 

Total amount of water in the tank in x minutes from now (including the initial 27.5 gallons of water) :

= 2x + 27.5

Therefore, the function which models the amount of water in the tank in x minutes from now :

W(x) = 2x + 27.5

To find the amount of water in 20 minutes from now, substitute x = 20 into the above function.

W(40) = 2(40) + 27.5

= 80 + 27.5

= 107.5

The amount of water in the tank in x minutes from now is 107.5 gallons.

Practice Questions

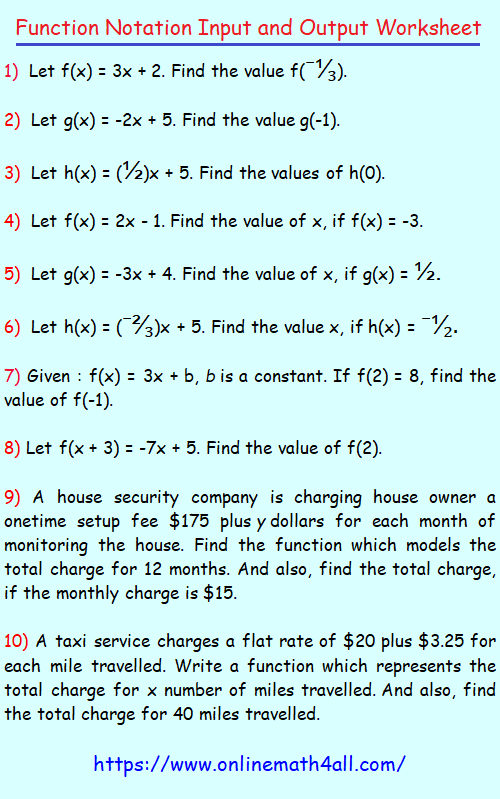
Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.