GRADE 10 MATH WORKSHEET

Problem 1 :

Find the equation of the straight line passing through the point (3, 2) and the perpendicular to the straight line joining the points (4, 5) and (1, 2).

Solution :

Slope of the line joining the points (4, 5) and (1, 2).

m  =  (y₂-y₁)/(x₂-x₁)

m  =   (2-5)/(1-4)

m  =  1

Slope of the required line  =  -1

Equation of the required line :

y-y₁  =  (-1/m)(x-x₁)

y-2  =  -1(x-3)

x+y-2-3  =  0

x+y-5  =  0

Problem 2 :

Find the point of intersection of the straight lines

x - y = 3 and x + y = 5

Solution :

x - y = 3  ------(1)

x + y = 5  ------(2)

(1) + (2)

2x  =  8

x  =  4

By applying the value of x in (1), we get

4-y  =  3

y  =  1

So, the point of intersection of the given lines is (4, 1).

Problem 3 :

Find the length of the chord of a circle of radius 3 cm subtending at the center angle of 144°.

Solution :

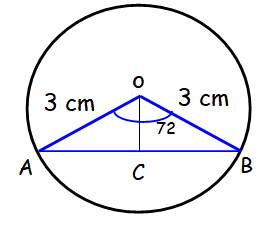
In triangle OCB,

sin θ  =  Opposite side / Hypotenuse

sin 72  =  BC/OB

0.9510  =  BC/3

BC  =  2.853

AB  =  2BC

AB  =  2(2.853)

AB  =  5.706

So, the length of chord is 5.706 cm.

Problem 4 :

The tree stands vertically on the bank of a river. From a point on the another bank directly opposite to the tree, the angle of elevation of the top of the tree is 60°. From the point 40 m behind this point on the same bank, the angle of elevation of the top of a tree is 30°. Find the height of the tree and the width of the river.

Solution :

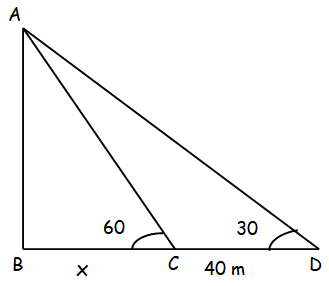
In triangle ABC,

tan θ  =  Opposite side / Adjacent side

tan 60  =  AB/BC

√3  =  AB/x

AB  =  x√3 -----(1)

tan 30  =  AB/BD

1/√3  =  AB/(x + 40)

AB  =  (x + 40)/√3 -----(2)

(1)  =  (2)

x√3  =  (x + 40)/√3

3x-x  =  40

x  =  20

By applying the value of x in (1), we get

AB  =  20√3 

AB  =  20(1.732)

AB  =  34.64

So, height of tree and width of the river are 34.64 m and 20 m respectively.

Problem 5 :

Find the range of the data

27, 28, 34, 36, 39, 50

Solution :

To find the range of the data, we use the formula

Range  =  Large value - small value

Range  =  50 - 27

Range  =  23

Problem 6 :

A group of 100 candidates have their average height 163.8 cm with coefficient of variation 3.2%. What is the standard deviation of their height?

Solution :

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

x̄  =  163.8, coefficient of variation  =  3.2%

(σ/x̄) ⋅ 100  =  3.2

(σ/163.8) ⋅ 100  =  3.2

σ  =  (3.2 ⋅ 163.8)/100

σ  =  5.2416

Problem 7 :

An integer is chosen at random from 1 to 50. Find the probability that the number is not divisible by 5.

Solution :

Sample space  =  {1, 2, 3, 4, 5, ...........50}

n(S)  =  50

Let A be the event of getting a number divisible by 5.

A  =  {5, 10, 15, 20, 25, 30, 35, 40, 45, 50}

n(A)  =  10

p(A)  =  n(A)/n(S)

p(A)  =  10/50  =  1/5

P(not divisible by 5)  =  1 - 1/5

  =  4/5

Problem 8 :

The height of right circular cone is 7 cm greater than its radius.The slant height is 8 cm greater than its radius. Find the curved surface area of the cone.

Solution :

Height  =  r + 7

Slant height (l)  =  8 + r

Curved surface area  =  πrl

l²  =  r² + h²

(8+r)²  =  r² + (7+r)²

64+16r+r²  =  r²+49+14r+r² 

r² -16r + 14r + 49 - 64  =  0

r² -2r-15  =  0

(r-5)(r+3)  =  0

r  =  5 and r  =  -3 (in admissible)

l  =  13

Curved surface area  =  π(5)(13)

=  65π cm³

Problem 9 :

Find the L.C.M of (x²-2x+1) and (x²+x-2)

Solution :

(x²-2x+1)  =   (x-1)(x-1)

(x²+x-2)  =  (x+2)(x-1)

Least common multiple is (x-1)²(x+2).

Problem 10 :

Find the sum of the series

2+4+6+8+........................+360

Solution :

2+4+6+8+........................+360

  =  2(1+2+3+4+...........+180)

Sum of natural numbers  =  n(n+1)/2

  =  2(180)(181/2)

  =  180(181)

  =  32580

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.