GRADE 7 MATH WORKSHEET ONLINE

Question 1 :

The L.C.M of two numbers is 495 and their H.C.F is 5. If the sum of the numbers is 100., then their difference is.

(A)  10              (B)    46               (C)  70

Solution :

Let "x" and "100 - x" be two numbers 

Always we have relationship between L.C.M and H.C.F

Product of two numbers   =  L.C.M ⋅ H.C.F

x (x - 100)  =  495 ⋅ 5

x² - 100 x  = 2475

x² - 100 x - 2475  =  0

(x - 45) (x - 55)  =  0

So, the two numbers are 45 and 55.

Difference between 55 and 45 is 10.

So, the answer is 10.

Question 2 :

Given that 5³ + 5³ + 5³ + 5³ + 5³ = 5 ^J and 3² + 3² + 3² = 3^N, what is the value of JN?

(A)  12              (B)    18               (C)  4

Solution :

So, JN  =  4(3)  =  12.

Question 3 :

The difference between the two positive whole numbers is 3.The sum of their squares is 117. Find the two numbers.

(A)  8 and 9           (B)    -9 and 6           (C)  7 and 3

Solution :

Let x and y be two numbers 

Difference between numbers  =  3

x - y   =  3

x  =  3 + y

Sum of their squares  =  117

x² + y²  =  117

(3 + y)² + y²  =  117

9 + 6y + y² + y²  =  117

2y² + 6y + 9 - 117  =  0

2y² + 6y - 108  =  0

Divide by 2,

y² + 3y - 54  =  0

(y + 9) (y - 6)  =  0

y  =  -9 and 6

Hence the required numbers are -9 and 6.

Question 4 :

Given that |(3 - a)| = 2, compute the sum of all possible values of a

(A)  1 and 5          (B)    2 and 4           (C)  3 and 4

Solution :

So, the possible values are 1 and 5.

Question 5 :

The surface area and the volume of a cube are numerically equal. Find its volume.

(A)  216 cu.units    (B)  343 cu.units     (C)  512 cu.units

Solution :

Surface area of cube =  Volume of cube 

6a²  =  a³

Divide by a² on both sides 

6  =  a

Volume of cube  =   a³

  =  6³  =  216 cubic units 

Question 6 :

How many positive whole numbers less than 100 are divisible by 3, but it is not divisible by 2.

(A)  17        (B)  18        (C)  12

Solution :

Multiplies of 3 are,

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99.

By eliminating the even numbers, we get

3, 9, 15, 18, 21, 27, 33, 39, 51, 57, 63, 69, 75, 81, 87, 93, 99.

So 17 numbers are less than 100 are divisible by 3, but it is not divisible by 2.

Question 7 :

How many multiples of 17 are there between 23 and 227?

(A)  17        (B)  18        (C)  15

Solution :

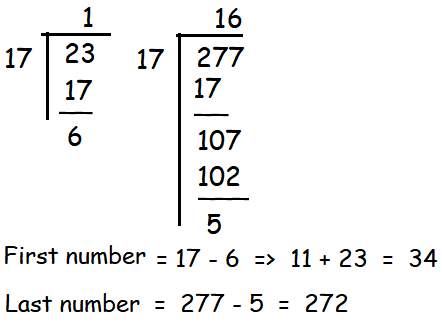
34, 51, ........, 272

a  =  34, d  =  17, l =  372

Number of terms  =  [(L - a) /d] + 1

  =  [(272 - 34)/17] + 1

  =  (238/17) + 1

  =  14 + 1

  =  15

So, the number of terms between 23 and 277 is 15.

Question 8 :

Compute the largest divisor of 2800 that is a perfect square

(A)  100        (B)  400        (C)  150

Solution :

In order to find the largest divisor, let us divide 2800 by each number. 

2800/100  =  28

2800/400  =  7

2800 is not divisible by 150.

So, the largest divisor is 400.

Question 9 :

Find the product of the integers from the number -5 to 5 inclusive.

Solution :

Numbers between -5 to 5.

-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5

In the above list we have 0. The product of any number by zero is 0.

So, the answer is 0.

Question 10 :

A particular number is doubled and the result is increased by 11 is 23. What is the original number? 

Solution :

Let x be the particular number

2x + 11  =  23

Subtract 11 on both sides

2x  =  23 - 11

2x  =  12

Divide 2 on both sides

x  =  6

So, the required number is 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.