GRAPHING SINE FUNCTIONS

The trigonometric ratios can also be considered as functions of a variable which is the measure of an angle. This angle measure can either be given in degrees or radians. 

Amplitude

The Amplitude is the height from the center line to the peak (or to the trough). Or we can measure the height from highest to lowest points and divide that by 2.

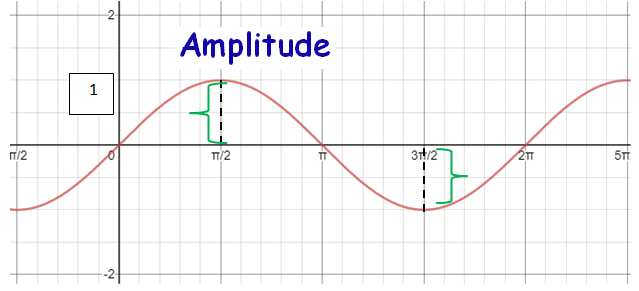
Period

The Period goes from one peak to the next (or from any point to the next matching point).

Period  =  2π/|b|

Frequency

The frequency is simply reciprocal of the period. It is the number of complete cycles the wave completes in unit interval.

Frequency  =  |b|/2π

Phase Shift

The Phase Shift is how far the function is shifted horizontally from the usual position.

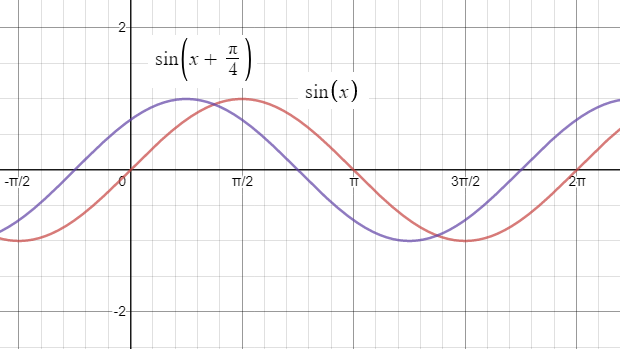
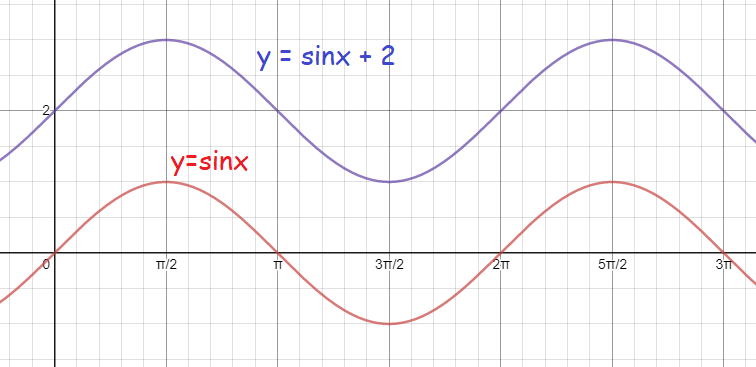
Vertical Shift

The Vertical Shift is how far the function is shifted vertically from the usual position.

Graphing Sine Functions

Example 1 :

Using degrees, find the amplitude and period of each function. Then graph.

y  =  sinx

Solution :

There is no phase shift and vertical shift. To find the points on the x axis, we need to divide the period by 4.

2π/4  =  π/2

So, the points on the x-axis are 0, π/2, π, 3π/2 and 2π.

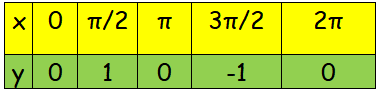
The points are (0, 0) (π/2, 1) (π, 0) (3π/2, -1) and (2π, 0)

Example 2 :

Find the amplitude, period and frequency of the of the function and use this information to sketch the graph of the function in the [-3π, 3π] by [-4, 4].

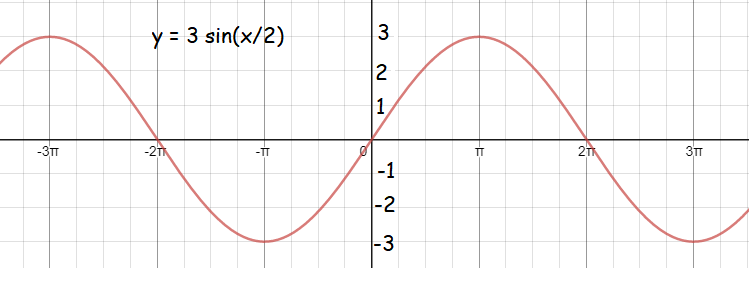
y  =  3sin (x/2)

Solution :

To find the points on the x axis, we need to divide the period by 4.

4π/4  =  π

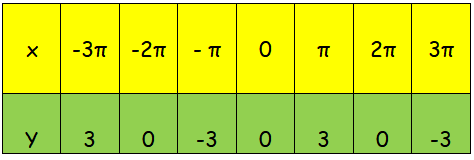
So, the points on the x-axis are 0, π, 2π, 3π and 4π. Since the graph starts from -3π, we need to start from -3π.

The points are (-3π, -3) (-2π, 0) (-π, -3) (0, 0) (π, 3) (2π, 0) and (3π, -3

Example 3 :

Find the amplitude, period and frequency of the of the function then graph the function.

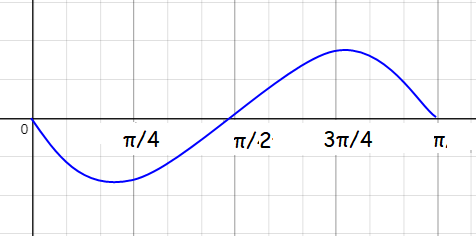
y  =  (-3/2)sin (2x)

Solution :

To find the points on the x axis, we need to divide the period by 4.

π/4

So, the points on the x-axis are 0, π/4, π/2, 3π/4 and π.

Without using technology, sketch the graphs of the following for 0 ≤ x ≤ 2π

Example 4 :

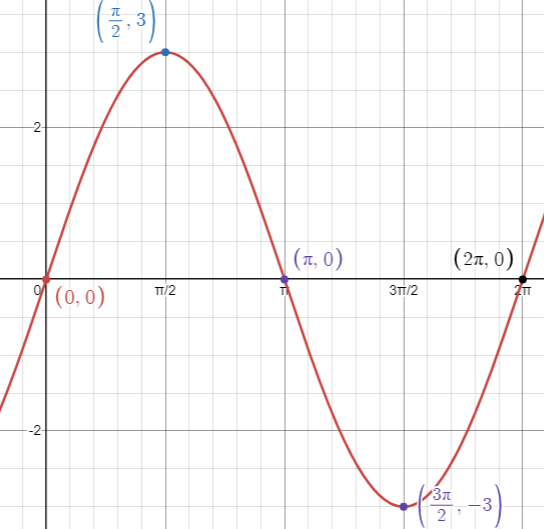
y = 3sin x

Solution :

y = 3sin x

y = a sin (bx + c) + d

Inputs are 0, π/2, π, 3π/2 and 2π

y = 3sin x

When x = 2π

y = 3 sin (2π)

y = 3 (0)

y = 0

So, the points are

(0, 0) (π/2, 3) (π, 0) (3π/2, -3) and (2π, 0)

Example 5 :

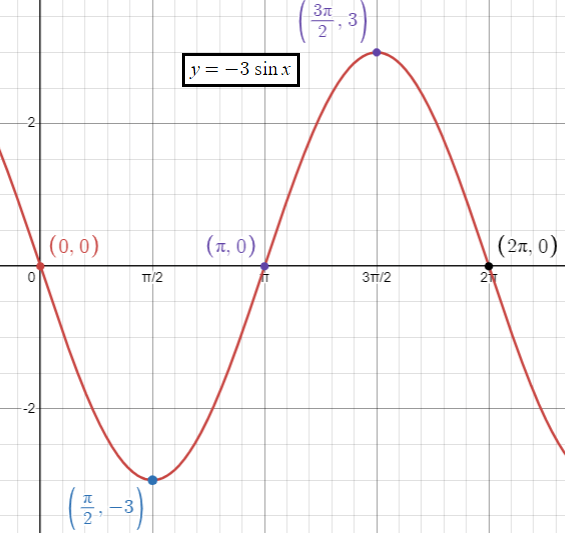
y = -3 sin x

Solution :

y = -3sin x

y = a sin (bx + c) + d

Since a is less than 0, there is reflection across x-axis.

Inputs are 0, π/2, π, 3π/2 and 2π

y = -3sin x

When x = 2π

y = -3 sin (2π)

y = -3 (0)

y = 0

So, the points are

(0, 0) (π/2, -3) (π, 0) (3π/2, 3) and (2π, 0)

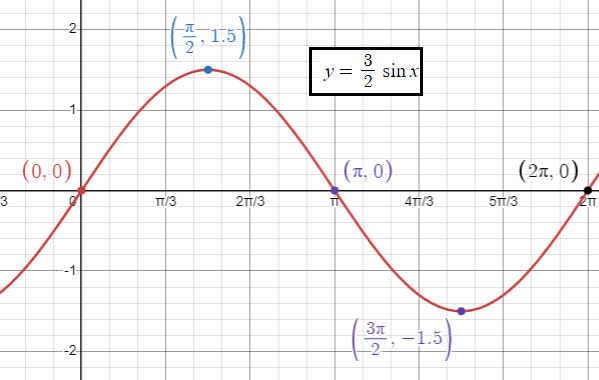
Example 6 :

y = (3/2) sin x

Solution :

y = (3/2) sin x

y = a sin (bx + c) + d

a > 0, there is no reflection.

Inputs are 0, π/2, π, 3π/2 and 2π

y = (3/2) sin x

When x = 2π

y = (3/2) sin (2π)

y = 3/2 (0)

y = 0

So, the points are

(0, 0) (π/2, 3/2) (π, 0) (3π/2, -3/2) and (2π, 0)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.