GRAPHING WITH INTERCEPTS

The following steps will be useful to graph a linear equation using intercepts.

Step 1 :

Find the x-intercept by letting y = 0 and solving for x. Use the x-intercept to plot the point where the line crosses the x-axis.

Step 2 :

Find the y-intercept by letting x = 0 and solving for y. Use the y-intercept to plot the point where the line crosses the y-axis.

Step 3 :

Draw a line through the two points.

Use intercepts to graph the line described by each equation.

Example 1 :

2x + 3y = 12

Solution :

x-intercept :

2x + 3y = 12

2x + 3(0) = 12

2x - 0 = 12

2x = 12

2x/2 = 12/2

x = 6

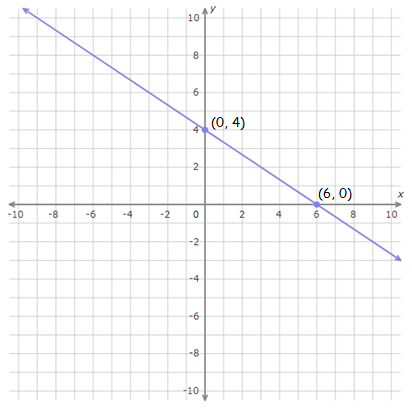
(6, 0)

y-intercept :

2x + 3y = 12

2(0) + 3y = 12

0 + 3y = 12

3y = 12

3y/3 = 12/3

y = 4

(0, 4)

Plot (6, 0) and (0, 4).

Connect with a straight line.

Example 2 :

5x - y - 10 = 0

Solution :

x-intercept :

5x - y - 10 = 0

5x - 0 - 10 = 0

5x - 10 = 0

5x = 10

5x/5 = 10/5

x = 2

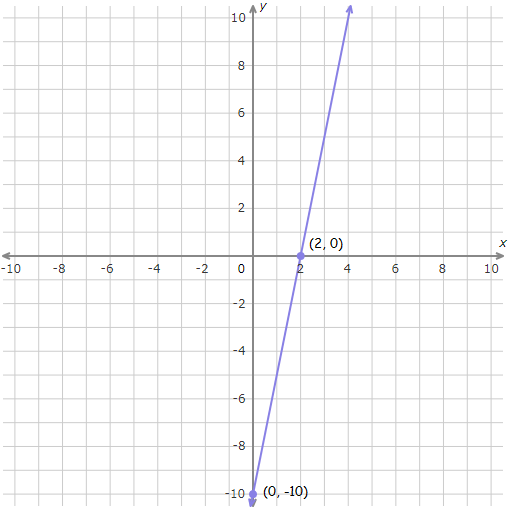
(2, 0)

y-intercept :

5x - y - 10 = 0

5(0) - y - 10 = 0

0 - y - 10 = 0

-y - 10 = 0

-y = 10

y = -10

(0, -10)

Plot (2, 0) and (0, -10).

Connect with a straight line.

Example 3 :

y = 4x - 4

Solution :

x-intercept :

y = 4x - 4

0 = 4x - 4

4 = 4x

1 = x

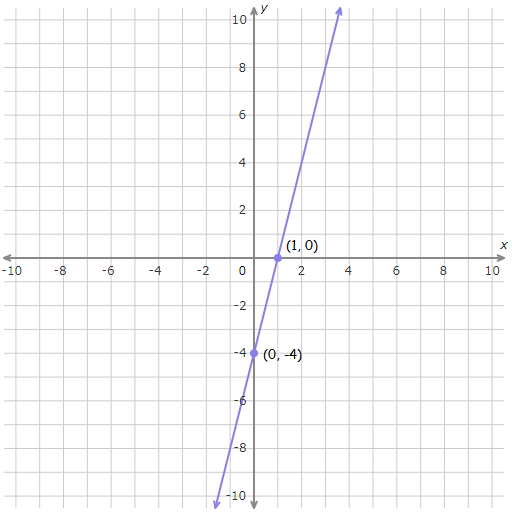
(1, 0)

y-intercept :

y = 4x - 4

y = 4(0) - 4

y = 0 - 4

y = -4

(0, -4)

Plot (1, 0) and (0, -4).

Connect with a straight line.

Example 4 :

y = -x/2 - 2

Solution :

x-intercept :

y = -x/2 - 2

0 = -x/2 - 2

2 = -x/2

-4 = x

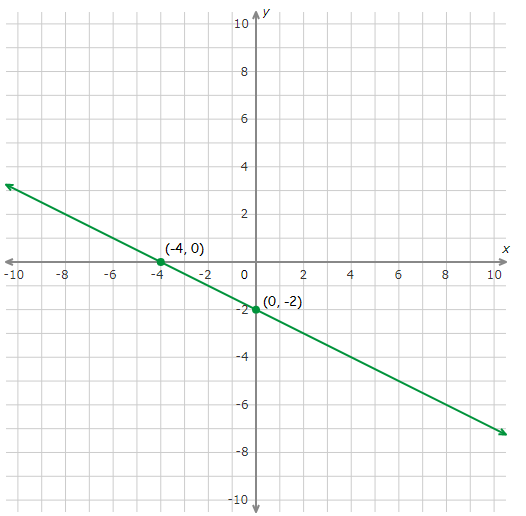
(-4, 0)

y-intercept :

y = -x/2 - 2

y = -(0)/2 - 2

y = 0 - 2

y = -2

(0, -2)

Plot (-4, 0) and (0, -2).

Connect with a straight line.

Example 5 :

The amount y (in gallons) of gasoline remaining in a gas tank after driving x hours is y = −2x + 12.

(a) Graph the equation.

(b) Interpret the x- and y-intercepts.

Solution :

y = −2x + 12

To graph the equation, we will find intercepts.

x-intercept :

Put y = 0

0 = -2x + 12

-2x = -12

x = 12/2

x = 6

y-intercept :

Put x = 0

y = -2(0) + 12

y = 12

x-intercept is 6 and y-intercept is 12.

a) Graphing the line :

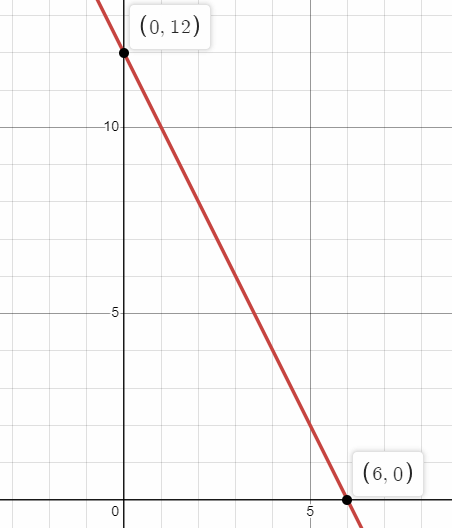
b) Interpreting the intercepts :

x = number of hours

y = amount of gasoline

After 6 hours, the quantity of remaining quantity gasoline will be 0.
Initially the amount of gasoline in the tank is 12.

c) When y = 5, x = ?

y = -2x + 12

5 = -2x + 12

5 - 12 = -2x

-7 = -2x

x = 7/2

x = 3.5 hours

So, after 3.5 hours amount of gasoline remaining is 5.

Example 6 :

You are downloading a song. The percent y (in decimal form) of megabytes remaining to download after x seconds is y = −0.1x + 1.

a. Graph the equation.

b. Interpret the x- and y-intercepts.

c. After how many seconds is the download 50% complete?

Solution :

y = -0.1x + 1

x-intercept :

Put y = 0

y = -0.1x + 1

0 = -0.1x + 1

-1 = -0.1x

x = 1/0.1

x = 10

y-intercept :

Put x = 0

y = -0.1x + 1

y = -0.1(0) + 1

y = 1

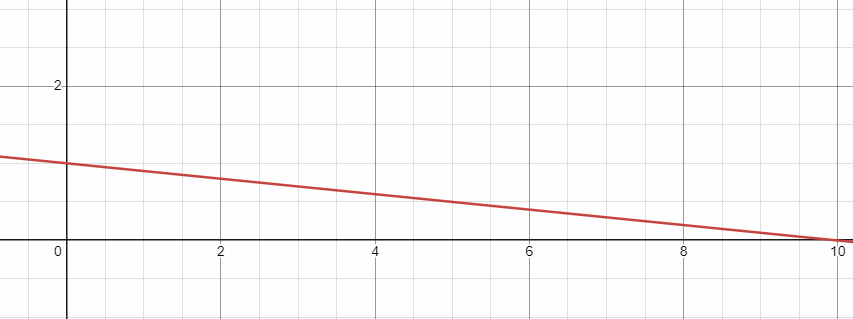
b) x- number of seconds

y- percentage of megabytes remaining to download

x-intercept is at (10, 0)

So, after 10 seconds the song can be downloaded completely.

y-intercept is at (0, 1)

At the beginning 1% of megabytes

c) When y = 50% or 0.5

0. 5 = -0.1x + 1

0.5 - 1 = -0.1x

-0.5 = -0.1x

x = 0.5/0.1

x = 5 seconds

After 5 seconds the download can be completed.

Example 7 :

The graph relates temperature y (in degrees Fahrenheit) to altitude x (in thousands of feet).

a. Find the slope and y-intercept.

b. Write an equation of the line.

c. What is the temperature at sea level?

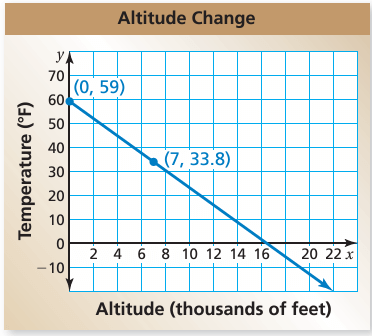
Solution :

a) The points on the line are (0, 59) and (7, 33.8)

m = (y2 - y1) / (x2 - x1)

= (33.8 - 59) / (7 - 0)

= -25.2 / 7

Slope (m) = -3.6

To find the y-intercept exactly, we use the formula

y = mx + b

y = -3.6x + b

Applying the point (0, 59)

59 = -3.6(0) + b

b = 59

So, the y-intercept is 59.

b) Equation of the line is y = -3.6x + 59

c) 59 degree is the temperature in sea level.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

GRAPHING WITH INTERCEPTS

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Digital SAT Math Problems and Solutions (Part - 90)

Digital SAT Math Problems and Solutions (Part - 89)