HOW TO CHECK IF EACH RELATION IS A FUNCTION

A relation f between two non-empty sets X and Y is called a function from X to Y if, for each x ∈ X there exists only one y ∈Y such that (x, y) ∈ f .

That is, f = {(x,y)| for all x ∈ X, y ∈ Y }.

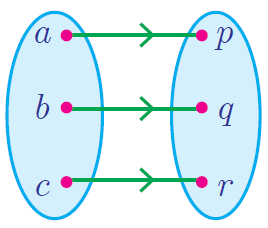	This represents a function. Each input corresponds to a single output.
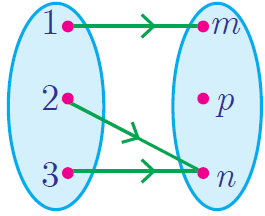	This represents a function. Each input corresponds to a single output.

Question 1 :

Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on ℕ. Find the domain, co-domain and range. Is this relation a function?

Solution :

Since x and y ∈ N, 

f = {(1, 2) (2, 4) (3, 6) (4, 8)................}

For each values of x, we get different values of y. So the given relation is a function.

Domain is the set of values of x

Domain  =  {1, 2, 3, 4, ............}

Co domain is the set of value of y. Since y ∈ N

Co domain  =  {1, 2, 3, 4, .............}

Range means the set of values of y, which are associated with x.

Range =  {2, 4, 6, 8, .....}

Question 2 :

Let X = {3, 4, 6, 8}. Determine whether the relation ℝ  = {(x, f (x)) | x ∈ X, f (x) = x² + 1} is a function from X to ℕ ?

Solution :

Given that :

 f (x) = x² + 1

 x ∈ X

R  =  { (3, 10) (4, 17) (6, 37) (8, 65) } 

For each values of x, we get different values of f(x). 

Hence it is a function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.