HOW TO CHECK IF THE GIVEN POINTS FORM A PARALLELOGRAM

To check, if the given points form a parallelogram, we can use one of the following properties of parallelogram

1. Lengths of opposite sides are equal.

2. Slopes of opposite sides are equal.

3. Diagonals bisect each other.

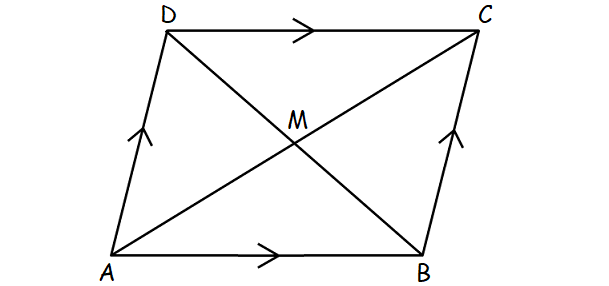
In the parallelogram above,

AB = DC  and  AD = BC

AB||DC  and  AD||BC

Mid-point of AC = Mid-point of BD

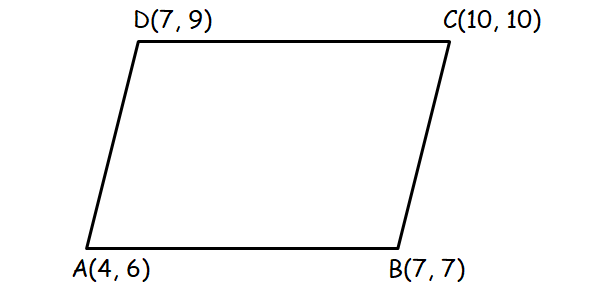
Example 1 :

Examine whether the points A(4, 6), B(7, 7), C(10, 10) and D(7, 9) form a parallelogram.

Solution :

Consider the two points (x₁, y₁) and (x₂, y₂) on the xy-plane.

Formula to find the distance between the two points : 

Length of AB :

Length of DC :

Length of AD :

Length of BC :

Example 2 :

ABCD is a quadrilateral where A(8, 4) and B(1, 3) and C(3, -1) and D(4, 6). Check, if ABCD is a parallelogram.

Solution :

Consider the two points (x₁, y₁) and (x₂, y₂) on the xy-plane.

Formula to find the mid-point of (x₁, y₁) and (x₂, y₂) : 

Mid-point of the diagonal AC :

Mid-point of the diagonal BD :

Mid-point of diagonal AC = Mid-point of diagonal BD

Therefore, ABCD is a parallelogram.

Example 3 :

Show that the given points form a parallelogram :

A(2.5, 3.5) , B(10,-4), C(2.5,-2.5) and D(-5,5)

Solution :

In a parallelogram, we can prove that the opposite sides are parallel by showing that the slopes of opposite sides are equal.

A(2.5, 3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5)

Slope of AB = Slope of CD

Slope of BC = Slope of DA

Therefore, the given points form a parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.