SURDS AND INDICES
Surds
Let a be a rational number and n be a positive integer such that
a1/n = n√a
Then, n√a is called a surd of order n.
Laws of Surds
Law 1 :
n√a = a1/n
Law 2 :
n√(ab) = n√a x n√b
Law 3 :
n√(a/b) = n√a / n√b
Law 4 :
(n√a)n = a
Law 5 :
m√(n√a) = mn√a
Law 6 :
(n√a)m = n√am
Laws of Indices
Law 1 :
xm ⋅ xn = xm+n
Law 2 :
xm ÷ xn = xm-n
Law 3 :
(xm)n = xmn
Law 4 :
(xy)m = xm ⋅ ym
Law 5 :
(x / y)m = xm / ym
Law 6 :
x-m = 1 / xm
Law 7 :
x0 = 1
Law 8 :
x1 = x
Law 9 :
xm/n = y -----> x = yn/m
Law 10 :
(x / y)-m = (y / x)m
Law 11 :
ax = ay -----> x = y
Law 12 :
xa = ya -----> x = y
Solved Problems
Problem 1 :
If x1/p = y1/q = z1/r and xyz = 1, then find the value of
(p + q + r).
Solution :
Let x1/p = y1/q = z1/r = k.
Then,
x1/p = k -----> x = kp
y1/q = k -----> y = kpq
z1/r = k -----> z = kr
Given : xyz = 1
Then,
xyz = 1
kp ⋅ kq ⋅ kr = 1
kp + q + r = 1 -----(1)
We know that a0 = 1.
So,
k0 = 1
In (1), substitute 1 = k0.
(1) -----> kp + q + r = k0
Using law 11 of indices, we get
p + q + r = 0
Problem 2 :
Simplify :
[1-{1-(1-x2)-1}-1]-1/2
Solution :
[1-{1-(1-x2)-1}-1]-1/2 :
= [1-{1-1/(1-x2)}-1]-1/2
= [1-{(1-x2-1)/(1-x2)}-1]-1/2
= [1-{-x2/(1-x2)}-1]-1/2
= [1-{x2/(x2-1)}-1]-1/2
= [1-(x2-1)/x2]-1/2
= [{x2-(x2-1)}/x2]-1/2
= [(x2-x2+1)/x2]-1/2
= [1/x2]-1/2
= [x2]1/2
= x
Problem 3 :
Using (a - b)3 = a3 - b3 - 3ab(a-b), if x = p1/3 - p-1/3, find the value of
x3 + 3x
Solution :
Given : x = p1/3 - p-1/3
Take power 3 on both the sides.
x3 = (p1/3 - p-1/3)3
Using (a - b)3 = a3 - b3 - 3ab(a - b).
x3 = (p1/3)3 - (p-1/3)3 - 3p1/3.p-1/3(p1/3-p-1/3)
x3 = p - p-1 - 3p1/3 - 1/3(x)
x3 = p - 1/p - 3p0x
x3 = p - 1/p - 3(1)x
x3 = p - 1/p - 3x
x3 + 3x = p - 1/p
Problem 4 :
Simplify :
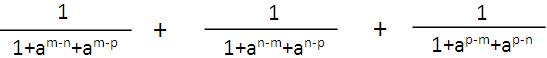
Solution :

Problem 5 :
If x = 31/3 + 3-1/3, find the value of
3x3 - 9x
Solution :
Given : x = 31/3 + 3-1/3
Take power 3 on both the sides.
x3 = (31/3 + 3-1/3)3
Using (a + b)3 = a3 + b3 + 3ab(a + b).
x3 = (31/3)3 + (3-1/3)3 + 3 ⋅ 31/3 ⋅ 3-1/3(31/3 + 3-1/3)
x3 = 3 + 3-1 + 3 ⋅ 31/3 - 1/3 ⋅x
x3 = 3 + 1/3 + 3 ⋅ 30 ⋅ x
x3 = 3 + 1/3 + 3(1)x
x3 = 3 + 1/3 + 3x
x3 - 3x = 3 + 1/3
Multiply each side by 3.
3(x3 - 3x) = 3(3 + 1/3)
3x3 - 9x = 9 + 1
3x3 - 9x = 10
Problem 6 :
If ax = b, by = c and cz = a, then find the value of xyz.
Solution :
Let
ax = b -----(1)
by = c -----(2)
cz = a -----(3)
Substitute a = cz in (1).
(1)-----> (cz)x = b
czx = b
Substitute c = by.
(by)zx = b
bxyz = b
bxyz = b1
xyz = 1
Problem 7 :
If 2x = 3y = 6-z, then find the value of
1/x + 1/y + 1/z
Solution :
Let 2x = 3y = 6-z = k.
Then,
2x = k -----> 2 = k1/x
3y = k -----> 3 = k1/y
6-z = k -----> 6 = k-1/z
And also,
6 = k-1/z
(2 x 3) = k-1/z
In (1), substitute 2 = k1/x, 3 = k1/y.
k1/x ⋅ k1/y = k-1/z
k1/x + 1/y = k-1/z
Using law 11 of indices, we get
1/x + 1/y = -1/z
1/x + 1/y + 1/z = 0
Problem 8 :
If (√9)-7 ⋅ (√3)-4 = 3k, then find the value of k.
Solution :
(91/2)-7 ⋅ (31/2)-4 = 3k
(9)-7/2 ⋅ (3)-4/2 = 3k
(32)-7/2 ⋅ 3-2 = 3k
32 ⋅ (-7/2) ⋅ 3-2 = 3k
3-7 ⋅ 3-2 = 3k
3-7 - 2 = 3k
3-9 = 3k
k = -9
So, the value of k is -9.
Problem 9 :
If √(x√x) = xa, then find the value of a.
Solution :
√(x√x) = xa
√(x ⋅ x1/2) = xa
√(x1 + 1/2) = xa
√(x3/2) = xa
(x3/2)1/2 = xa
x3/4 = xa
3/4 = a
So, the value of a is 3/4.
Problem 10 :
If n3 = x, n4 = 20x and n > 0, then find the value of n.
Solution :
n4 = 20x
n3 ⋅ n = 20x
Substitute x for n3.
x ⋅ n = 20x
nx = 20x
Divide each side by x.
n = 20
So, the value of n is 20.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Worksheet on Proving Trigonometric Identities
Nov 02, 24 11:58 PM
Worksheet on Proving Trigonometric Identities -
AP Precalculus Problems and Solutions (Part - 1)
Oct 30, 24 10:07 AM
AP Precalculus Problems and Solutions (Part - 1) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Oct 29, 24 06:24 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
