HOW TO DETERMINE THE RULE OF A SEQUENCE

The sequence is the number arrangements, that follows a particular rule. By analyzing the sequence given we can find the rule followed in the sequence.

Find the rule which will generate the sequence :

Example 1 :   

4, 7, 10, 13, 16, ……

Solution :

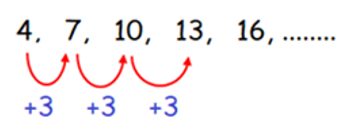
By observing the sequence above, every term is

added by +3 

to get the next term of the sequence.

Example 2 :

- 2, 3, 8, 13, 18, ……

Solution :

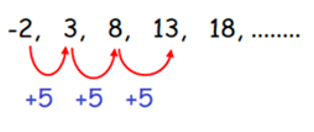
By observing the sequence above, every term is

added by +5

to get the next term of the sequence.

Example 3 :

1, 7, 13, 19, 25, ……

Solution :

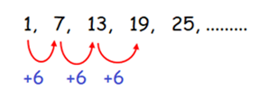
By observing the sequence above, every term is

added by +6

to get the next term of the sequence.

Example 4 :

3,  10,  17,  24,  31, ……

Solution :

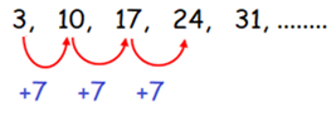
By observing the sequence above, every term is

added by +7

to get the next term of the sequence.

Example 5 :

40,  37,  34,  31, ……

Solution :

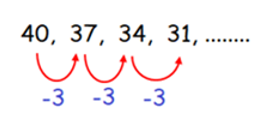
By observing the sequence above, every term is

subtracted by -3

to get the next term of the sequence.

Example 6 :

76, 72, 68, 64, ……

Solution :

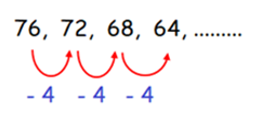
By observing the sequence above, every term is

subtracted by -4

to get the next term of the sequence.

Example 7 :

8, 3, -2, -7, ……

Solution :

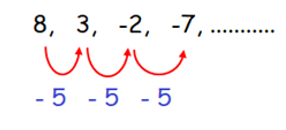
By observing the sequence above, every term is

subtracted by -5

to get the next term of the sequence.

Example 8 :

127, 121, 115, 109, ……

Solution :

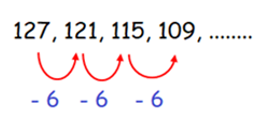
By observing the sequence above, every term is

subtracted by -6

to get the next term of the sequence.

Example 9 :

1/3,  2/5,  3/7,  4/9,  5/11 ……

Solution :

By observing the given sequence,

numerators  =  consecutive numbers

denominators  =  odd numbers

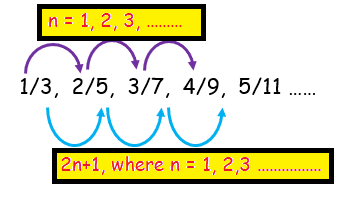
Numerator :

If n be the numerator,

n  =  natural numbers starts with 1

Denominator :

odd numbers  =  starts with 3

denominator  =  2n+1 

n  =  1, 2, 3,........

2n+1  =  3, 5, 7, .......

So, the rule is n/(2n+1)

Example 10 :

Four sequences A, B, C and D are defined by the following formulae

A : U_n = 8n + 2

B : U_n = 7n - 3

C : U_n = 3n + 1

D : U_n = 100 - 6n

a)  Which sequence have 4 as their first term ?

b)  Which sequence is decreasing ?

c) Which sequence has a difference of 7 between terms ?

d) Which sequence has 301 as its 100^th term ?

Solution :

a) Let us find the first term of the sequence B.

B : U_n = 7n - 3

To find the first term, let us apply n = 1

U₁ = 7(1) - 3

= 7 - 3

U₁ = 4

b)  By observing the rules of each sequence, from the initial value 100 some quantity is subtracted every time. To confirm this, let us find some of the terms.

D : U_n = 100 - 6n

So, sequence D is the decreasing sequence.

c)  Let us find first three terms of the sequence B,

U_n = 7n - 3

So, in sequence B the difference between two terms is 7

d)  Let us find the 100th term in sequence C.

C : U_n = 3n + 1

When n = 100

 U₁₀₀ = 3(100) + 1

= 300 + 1

= 301

So, 100th term of sequence C is 301.

Example 11 :

Look at the part of the number line, write down the 2 missing numbers.

Copy and complete the sentence

The numbers on this line go up in steps of _______

Solution :

-7, ____, 1, 5, 9, _____, 17

By observing 1, 5 and 9 every term is increased by 4. Then after 9, we have to add 4 by 9. Then 14 is the term after 9.

Before 1, we have to decrease 4, then 1 - 4 = -3. So, after -7 we have -3.

Then the missing terms are -3 and 14.

Example 12 :

Jeff makes a sequence of patterns with black and grey triangular tiles.

The rule of finding the number of tiles pattern number N in Jeff's sequence is

Number of tiles = 1 + 3N

i)  The 1 in this rule represents the black tile. What does the 3N represent ?

ii)  Jeff makes pattern number 12 in this sequence. How many black tiles and how many grey tiles does he use ?

iii)  Jeff uses 61 tiles altogether to make a pattern in his sequence, what is the number of pattern he makes ?

Solution :

i) Here by observing the pattern, 3N says the number of grey tiles.

ii)  Number of tiles = 1 + 3N

To find number of tiles in the 12th pattern, we have to apply N = 12

Number of tiles = 1 + 3(12)

= 1 + 36

= 37

So, in the 12th pattern number of black tiles is 1 and number of grey tiles = 36.

iii)  When number of tiles = 61

61 = 1 + 3N

61 - 1 = 3N

3N = 60

N = 60/3

N = 20

So, total number of tiles in the 20th pattern is 61.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.