HOW TO FIND HCF OF TWO NUMBERS IN DECIMAL

The largest number which can divide the given two or more numbers evenly is called their highest common factor (HCF).

In this section, we will learn, how to find highest common factor of two or more numbers in decimal.

The following steps would be useful to find HCF of two numbers in decimal.

Example 1 :

Find the highest common factor of 0.90 and 0.30.

Solution :

In the given two numbers 0.90 and 0.30, we find equal number of digits after the decimal point in both the numbers. That is, two digits.

To get rid of the decimal point, we have to multiply each number by 100.

0.90 ⋅ 100 = 90

0.30 ⋅ 100 = 30

Find the HCF of 90 and 30.

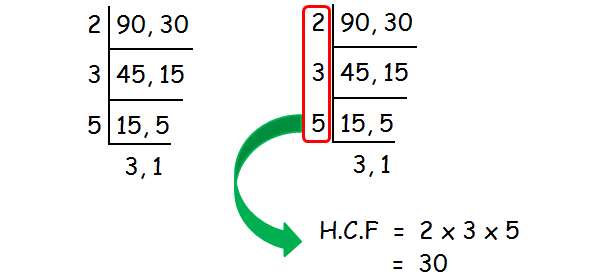
HCF of 90 and 30 is 30.

Divide the HCF by 100.

30/100 = 0.3

So, the highest common factor of 0.90 and 0.30 is 0.3.

Example 2 :

Find the highest common factor of 0.36 and 0.27.

Solution :

In the given two numbers 0.36 and 0.27, we find equal number of digits after the decimal point in both the numbers. That is, two digits. 

To get rid of the decimal point, we have to multiply each number by 100.

0.36 ⋅ 100 = 36

0.27 ⋅ 100 = 27

Find the HCF of 36 and 27.

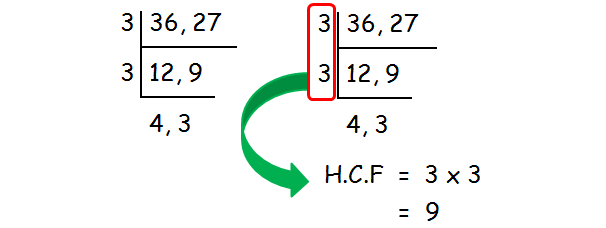
HCF of 36 and 27 = 9.

Divide the HCF by 100.

9/100 = 0.09

So, the highest common factor of 0.36 and 0.27 is 0.09.

Example 3 :

Find the highest common factor of 0.75 and 0.45.

Solution :

In the given two numbers 0.75 and 0.45, we find equal number of digits after the decimal point in both the numbers. That is, two digits. 

To get rid of the decimal point, we have to multiply each number by 100.

0.75 ⋅ 100 = 75

0.45 ⋅ 100 = 45

Find the HCF of 75 and 45.

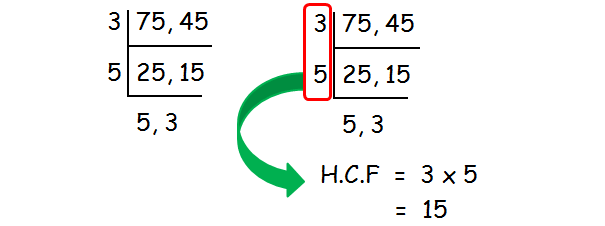
HCF of 75 and 45 is 15.

Divide the HCF by 100.

15/100 = 0.15

So, the highest common factor of 0.75 and 0.45 is 0.15.

Example 4 : 

Find the highest common factor of 0.36 and 0.72.

Solution :

In the given two numbers 0.36 and 0.72, we find equal number of digits after the decimal point in both the numbers. That is, two digits. 

To get rid of the decimal point, we have to multiply each number by 100.

0.36 ⋅ 100 = 36

0.72 ⋅ 100 = 72

Find the HCF of 36 and 72.

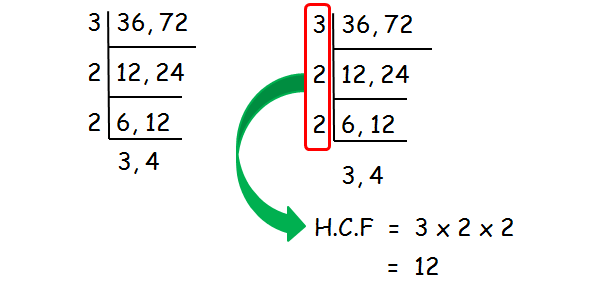
HCF of 36 and 72 is 12.

Divide the HCF by 100.

12/100 = 0.12

So, the highest common factor of 0.36 and 0.72 is 0.12.

Example 5 :

Find the highest common factor of 0.72 and 0.63.

Solution :

In the given two numbers 0.72 and 0.63, we find equal number of digits after the decimal point in both the numbers. That is, two digits. 

To get rid of the decimal point, we have to multiply each number by 100.

0.72 ⋅ 100 = 72

0.63 ⋅ 100 = 63

Find the HCF of 72 and 63.

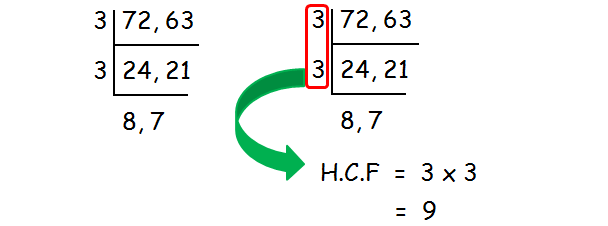
HCF of 72 and 63 is 9.

Divide the HCF by 100.

9/100 = 0.09

So, the highest common factor of 0.36 and 0.72 is 0.09.

Example 6 :

Find the greatest number which when divides 259 and 465 leaves remainders 4 and 6 respectively.

Solution :

To find the greatest number that divides 259 and 465 and leaving the remainders 4 and 6.

259 - 4 = 255

465 - 6 = 459

HCF = 3 x 17

= 51

So, the required number which when divides 259 and 465 leaves remainders 4 and 6 respectively is 51.

Example 7 :

Find the greatest number, which when divides 41, 71 and 91, leaves the same remainder in each case.

Solution :

Take the difference between all the three pairs of numbers and their HCF will be the answer i.e. 91 – 41 = 50, 71 – 41 = 30 and 91 – 71 = 20. Now, the HCF of 50, 30 and 20 is 10.

Sometimes in such questions, the common remainder can also be asked. You can divide any of the numbers given by HCF (41 ¸ 10) and find the remainder to be equal to 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.