HOW TO FIND LENGTH OF PERPENDICULAR FROM A POINT TO A LINE

Here we are going to see how to find the length of perpendicular from a point to a line.

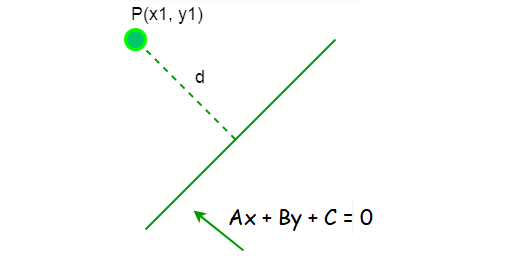
Distance between the point and a line

  =  |Ax + By + C|/√A² + B²

Question 1 :

If p₁ and p₂ are the lengths of the perpendiculars from the origin to the straight lines x sec θ + y cosec θ = 2a and x cos θ − y sin θ = a cos 2θ, then prove that p₁²+ p₂²= a².

Solution :

Length of perpendicular from origin (0, 0)  to the straight lines x sec θ + y cosec θ = 2a   :

  =  |((0)sec θ + (0)cosec θ - 2a)| /  √(secθ)² + (cosecθ)²

p₁  =  2a /  √(sec²θ) + (cosec²θ)

Taking squares on both sides, we get

p₁²  =  4a² / (sec²θ + cosec²θ)  ----(1)

Length of perpendicular from origin (0, 0)  to the straight lines  x cos θ − y sin θ = a cos 2θ  :

  =  |(0) cos θ - (0) sin θ - a cos 2θ)| /  √(sinθ)² + (cosθ)²

p₂  =  a cos 2θ /  √(sin²θ + cos²θ)

p₂  =  a cos 2θ /  1

p₂²  =  a² cos²2θ   ----(2)

p₁²  + p₂² =  4a² / (sec²θ + cosec²θ) + (a² cos²2θ)

sec θ =  1/cos θ, cosec θ =  1/sin θ &

cos 2θ = cos²θ - sin²θ  

  =  4a² (sin²θ cos²θ) + a² (cos²θ - sin²θ)²

  =  4a² (sin²θ cos²θ) + a² [cos⁴θ + sin⁴θ - 2sin²θ cos²θ]

  =  4a² sin²θ cos²θ + a² cos⁴θ + a²sin⁴θ - 2a²sin²θ cos²θ

  =  a² cos⁴θ + a²sin⁴θ + 2a²sin²θ cos²θ

  =  a² [sin²θ + cos²θ]²

  =  a² (1) 

  =  a²

Hence proved.

Question 2 :

Find the distance between the parallel lines

(i) 12x + 5y = 7 and 12x + 5y+7 = 0

(ii) 3x − 4y+5 = 0 and 6x − 8y − 15 = 0.

Solution :

Distance between two parallel lines  =  |C₁ - C₂|/√A² + B²

Since the given lines are parallel, coefficients of x and y terms will be equal in both the equations.

C₁  =  -7, C₂  =  7, A  =  12, B  =  5

 =  |-7 - 7|/√12² + 5²

 =  |-14|/√144 + 25

 =  14/√169

 =  14/13

Solution :

Distance between two parallel lines  =  |C₁ - C₂|/√A² + B²

In order to convert the coefficients of x and y terms as same as first equation, we have to divide the second equation by 2. 

C₁  =  5, C₂  =  -15/2, A  =  3, B  =  -4

 =  |5 + (15/2)|/√3² + (-4)²

 =  |25/2|/√9 + 16

 =  (25/2)/√25

 =  (25/2)/5  =  5/2

Question 3 :

Find the family of straight lines (i) Perpendicular (ii) Parallel to 3x + 4y − 12 = 0.

Solution :

Line which is perpendicular to the given line 3x + 4y − 12 = 0.

4x - 3y + k  =  0  and K ∈ R

Line which is parallel to the given line 3x + 4y − 12 = 0.

3x + 4y + k  =  0  and K ∈ R

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.