HOW TO FIND RANGE AND COEFFICIENT OF RANGE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The difference between the largest value and the smallest value is called Range.
Range = L – S
Coefficient of range is the relative measure of range.
Coefficient of range = (L - S)/(L + S)
where L is Large value and S is Small value.
Example 1 :
Find the range and coefficient of range of the following data.
(i) 63, 89, 98, 125, 79, 108, 117, 68
Solution :
L - 125 and S = 63
Range = L - S
= 125 - 63
Range = L - S = 62
Coefficient of range = (L - S)/(L + S)
L + S = 125 + 63 = 188
Coefficient of range = 62/188
= 31/94
= 0.33
(ii) 43.5, 13.6, 18.9, 38.4, 61.4, 29.8
L - 61.4 and S = 13.6
Range = L - S
= 61.4 - 13.6
Range = L - S = 47.8
Coefficient of range = (L - S)/(L + S)
L + S = 61.4 + 13.6 = 75
Coefficient of range = 47.8/75
= 478/750
= 0.64
Example 2 :
If the range and the smallest value of a set of data are 36.8 and 13.4 respectively, then find the largest value.
Solution :
Range = 36.8, smallest value (S) = 13.4
Range = L - S
36.8 = L - 13.4
L = 36.8 + 13.4
L = 50.2
Hence the largest value is 50.2.
Example 3 :
Calculate the range of the following data.
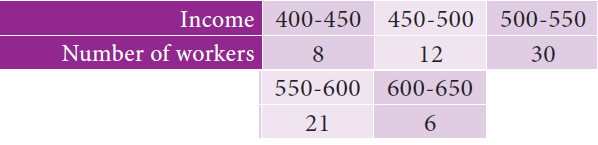
Solution :
Range = 650 - 400
= 250
Example 4 :
A teacher asked the students to complete 60 pages of a record note book. Eight students have completed only 32, 35, 37, 30, 33, 36, 35 and 37 pages. Find the standard deviation of the pages yet to be completed by them.
Solution :
Arranging the given data in ascending order, we get
30, 32, 33, 35, 35, 36, 37, 37.
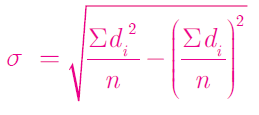
|
x 30 32 33 35 35 36 37 37 |
d = x - A d = x - 35 -5 -3 -2 0 0 1 2 2 Σd = -5 |
d2 25 9 4 0 0 1 4 4 Σd2 = 47 |
Σd2/8 = 47/8
(Σd/8)2 = (-5/8)2 = 25/64
σ = √(47/8) - (25/64)
σ = √(376 - 25)/64
σ = √351/64
σ = √5.48
σ = 2.34
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

