HOW TO FIND THE SLOPE OF ALTITUDE OF A TRIANGLE

In the Δ ABC shown below,

AD ⊥ BC, BE ⊥ AC, CF ⊥ AB

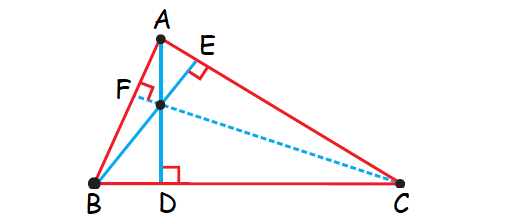
The line segments AD, BE and CF are called altitudes of the triangle ABC.

Since AD ⊥ BC, product of slopes of AD and BC is equal to -1.

slope of AD x slope of BC = -1

slope of AD = -1/slope of BC

Similarly,

slope of BE = -1/slope of AC

slope of CF = -1/slope of AB

Example :

Let A(1, 2), B(-4, 5) and C(0, 1) be the vertices of the Δ ABC. Find the slopes of the altitudes AD, BE and CF.

Solution :

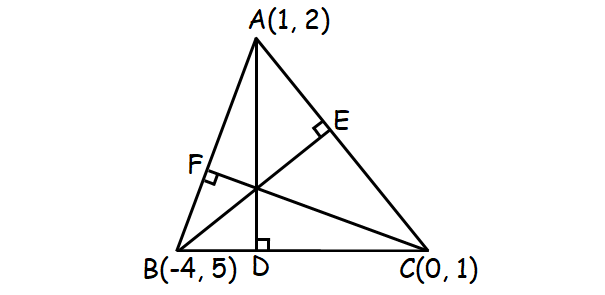
Slope of AD :

Use slope formula and find the slope of BC.

m = (y₂- y₁)/(x₂- x₁)

Substitute (x₁, y₁) = B(-4, 5) and (x₂, y₂) = C(0, 1).

slope of BC = (1 - 5)/(0 + 4)

= -4/4

= -1

slope of AD = -1/slope of BC

= -1/(-1)

= 1

Slope of BE :

m = (y₂- y₁)/(x₂- x₁)

Substitute (x₁, y₁) = A(1, 2) and (x₂, y₂) = C(0, 1).

slope of AC = (1 - 2)/(0 - 1)

= -1/(-1)

= 1

slope of BE = -1/slope of AC

= -1/1

= -1

Slope of CF :

m = (y₂- y₁)/(x₂- x₁)

Substitute (x₁, y₁) = A(1, 2) and (x₂, y₂) = B(-4, 5).

slope of AB = (5 - 2)/(-4 - 1)

= 3/(-5)

= -3/5

slope of CF = -1/slope of AB

= -1/(-3/5)

= 5/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

Recent Articles