HOW TO FIND THE DETERMINANT OF A 4X4 MATRIX

Example 1 :

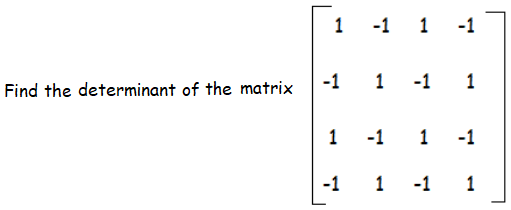
Solution :

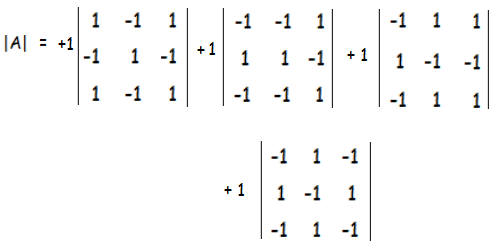
Let 3x3 matrix as M₁, M₂, M₃, and M₄

|A|  =  1M₁ + 1M₂ + 1M₃ + 1M₄ -----(1)

Now, we calculating M₁, M₂, M₃, and M₄

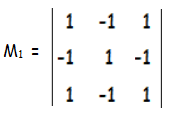
M₁  =  1(1 - 1) + 1(-1 + 1) + 1(1 - 1)

=  1(0) + 1(0) + 1(0)

M₁ =  0

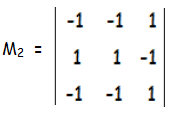
M₂  =  -1(1 - 1) + 1(1 - 1) + 1(-1 + 1)

=  -1(0) + 1(0) + 1(0)

M₂ =  0

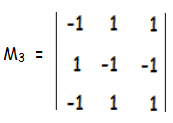
M₃  =  -1(-1 + 1) - 1(1 - 1) + 1(1 - 1)

=  -1(0) - 1(0) + 1(0)

M₃ =  0

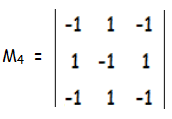
M₄  =  -1(1 - 1) - 1(-1 + 1) + 1(1 - 1)

=  -1(0) - 1(0) + 1(0)

M₄ =  0

By applying M₁, M₂, M₃, and M₄ values in equation (1), we get

|A|  =  1M₁ + 1M₂ + 1M₃ + 1M₄ 

=  1(0) + 1(0) + 1(0) + 1(0)

|A| =  0

So, the determinant of A is 0

Example 2 :

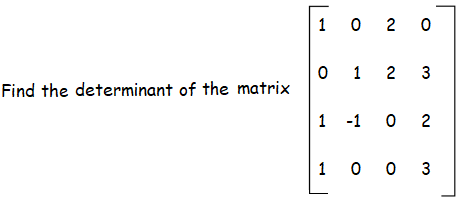
Solution :

Let 3x3 matrix as M₁, M₂, M₃, and M₄

|A|  =  1M₁ - 0M₂ + 2M₃ - 0M₄ -----(1)

Now, we calculating M₁, M₂, M₃, and M₄

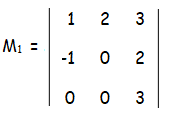
M₁  =  1(0 - 0) - 2(-3 - 0) + 3(0 - 0)

=  0 + 6 + 0

M₁ =  6

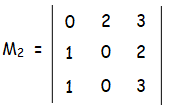
M₂  =  0(0 - 0) - 2(3 - 2) + 3(0 - 0)

=  0 - 2 + 0

M₂ =  - 2

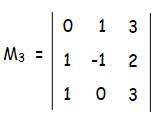
M₃  =  0(-3 - 0) - 1(3 - 2) + 3(0 + 1)

=  0 - 1 + 3

M₃ =  2

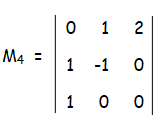
M₄  =  0(0 - 0) - 1(0 - 0) + 2(0 + 1)

=  0 + 0 + 2

M₄ =  2

By applying M₁, M₂, M₃, and M₄ values in equation (1), we get

|A|  =  1M₁ - 0M₂ + 2M₃ - 0M₄ 

=  1(6) - 0(-2) + 2(2) - 0(2)

=  6 + 4

|A| =  10

So, the determinant of A is 10

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.