HOW TO FIND THE MISSING COORDINATES OF A TRIANGLE

We may follow the steps given below to find the missing coordinate of a triangle when its area is given.

Step 1 :

Take the given points as (x₁, y₁) (x₂, y₂) and (x₃, y₃).

Step 2 :

Use the formula for area of triangle and apply the above values.

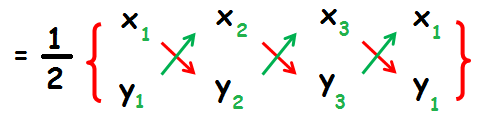
Step 3 :

Equate them to the given area, and solve for unknown.

Example 1 :

Find the value of "k" for which the given points are collinear.

(k, -1)  ( 2, 1) and (4, 5)

Solution :

If the given points are collinear then the area of triangle is zero

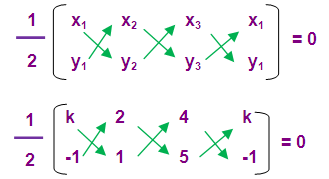
(1/2) [(k + 10 – 4) – (-2 + 4 + 5k)]  =  0

Multiply by 2 on both sides,

(k + 6) – (2 + 5k)  =  0

(k + 6 – 2 - 5k) = 0

-4 k + 4  =  0

-4k  =  -4

k  =  (-4)/(-4)

k  =  1

Example 2 :

Find the value of "k" for which the given points are collinear.

(2, -5)  (3, -4) and (9, k)

Solution :

If the given points are collinear then the area of triangle is zero.

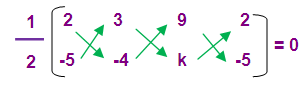
(1/2) [(-8 + 3k – 45) – (-15 - 36 + 2k)] = 0

Multiply by 2 on both sides,

(3k - 53) – (-51+ 2k)  =  0 x 2

(3k - 53 + 51- 2k)  =  0

 k - 2  =  0

 k  =  2

Example 3 :

Find the value of "k" for which the given points are collinear.

(k, k)  (2, 3) and (4, -1)

Solution :

If the given points are collinear then the area of triangle is zero.

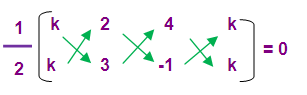
(1/2) [(3k - 2 + 4k) – (2k + 12 - k)] = 0

Multiply by 2 on both sides

[(7k - 2) – (k+12)] = 0 x 2

(7k - 2 – k - 12) = 0

6 k - 14 = 0

6k = 14

k = 14/6  

k = 7/3

Example 4 :

Vertices of the triangle taken in order and its area is 17 square units, find the value of a.

(0, 0)  (4, a) and (6, 4)

Solution :

If the given points are collinear then the area of triangle is zero.

Area of triangle  =  17 sq.units

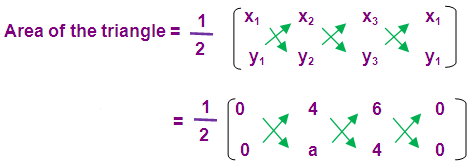
(1/2) [ (0 + 16 + 0) – (0 + 6 a + 0)]  =  17

(1/2)(16 – 6 a)  =  17

(1/2) x 2 (8 - 3a)  =  17

8 – 3 a  =  17

-3a  =  17 – 8

-3a  =  9

a  =  9/(-3)

a  =  -3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.