HOW TO FIND THE NEXT THREE TERMS IN ARITHMETIC SEQUENCE

Example 1 :

Find the next three terms of each arithmetic sequence.

4, 7, 10, 13, …

Solution :

Common difference :

d  =  a₂ - a₁

  =  7 - 4

  =  3

In order to get 5^th term, we have to add the common difference 3 with the 4^th term.

Hence the next three terms of the above sequence are 16, 19 and 21.

Example 2 :

Find the next three terms of each arithmetic sequence.

18, 24, 30, 36, …

Solution :

Common difference :

d  =  a₂ - a₁

  =  24 - 18

  =  6

In order to get 5^th term, we have to add the common difference 3 with the 4^th term.

Hence the next three terms of the above sequence are 42, 48 and 54.

Example 3 :

Find the next three terms of each arithmetic sequence.

-66, -70, -74, -78, …

Solution :

Common difference :

d  =  a₂ - a₁

  =  -70 - (-66)

  =  -70 + 66

=  -4

In order to get 5^th term, we have to add the common difference 3 with the 4^th term.

Hence the next three terms of the above sequence are -82, -86, and -90.

Example 4 :

Find the next three terms of each arithmetic sequence.

-31, -22, -13, -4, …

Solution :

Common difference :

d  =  a₂ - a₁

  =  -22 - (-31)

  =  -22 + 31

=  9

In order to get 5^th term, we have to add the common difference 3 with the 4^th term.

Hence the next three terms of the above sequence are 5, 14 and 23.

Example 5   :

Online bidding for a purse increases by $5 for each bid after the $60 initial bid.

a. Write a function that represents the arithmetic sequence.

b. Graph the function.

c. The winning bid is $105. How many bids were there?

Solution :

a.

f_n = a + (n - 1) d

f_n = 60 + (n - 1) (65 - 60)

= 60 + (n - 1) (5)

= 60 + 5n - 5

= 55 + 5n

So, the required function which represents the sequence is 55 + 5n.

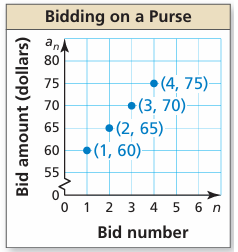
c. Amount of winning bid = 105

105 = 55 + 5n

Solving for n, we get

5n = 105 - 55

5n = 50

n = 50/5

n = 10

So, there were 10 bids.

Example 6 :

A carnival charges $2 for each game after you pay a $5 entry fee.

a. Write a function that represents the arithmetic sequence.

b. Graph the function.

c. How many games can you play when you take $29 to the carnival?

Solution :

a)  f_n = a + (n - 1) d

a = 7, d = 9 - 7 ==> 2

f_n = 7 + (n - 1) 2

= 7 + 2n - 2

f_n = 5 + 2n

b)

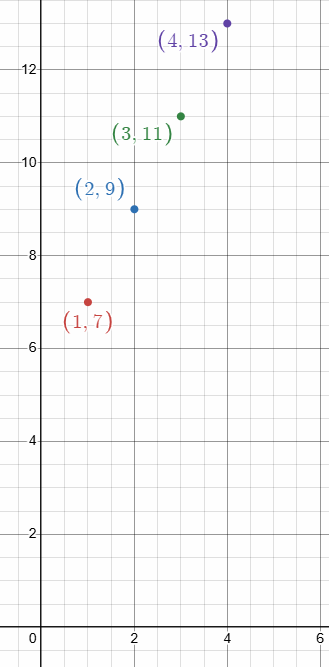
c) f_n = 5 + 2n

amount spent for playing games = $29

29 = 5 + 2n

2n = 29 - 5

2n = 24

n = 24/2

n = 12

So, you may play 12 games.

Example 7 :

Write a sequence that represents the number of smiley faces in each group. Is the sequence arithmetic? Explain

Solution :

Number of smiley faces,

4, 6, 8, 10, ...............

Each term is increased by 2. So, this sequence represents arithmetic.

Example 8 :

The total number of babies born in a country each minute after midnight January 1st can be estimated by the sequence shown in the table.

a. Write a function that represents the arithmetic sequence.

b. Graph the function.

c. Estimate how many minutes after midnight January 1st it takes for 100 babies to be born.

Solution :

a)

f_n = a + (n - 1) d

a = 5, d = 10 - 5 ==> 5

f_n = 5 + (n - 1) 5

= 5 + 5n - 5

f_n = 5n

b)

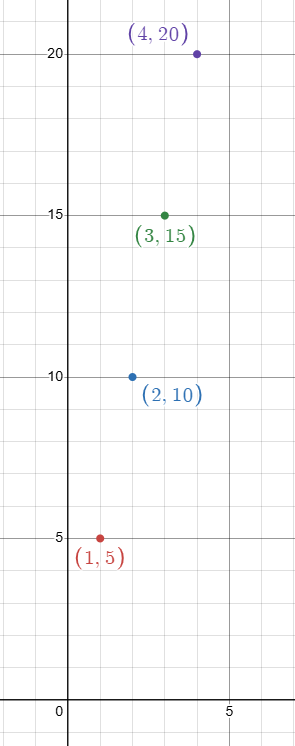
c) 

f_n = 5n

Here f_n = 100

100 = 5n

n = 100/5

n = 20

So, the required number of minutes is 20.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.