HOW TO FIND THE ORDER OF PRODUCT OF TWO MATRICES

Question 1 :

Find the order of the product matrix AB if

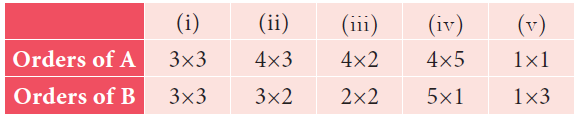
Solution :

(i)  Order of A is 3 x 3, order of B is 3 x 3.

The order of the matrix AB is 3 x 3.

(ii)  Order of A is 4 x 3, order of B is 3 x 2.

The order of the matrix AB is 4 x 2.

(iii)  Order of A is 4 x 2, order of B is 2 x 2.

The order of the matrix AB is 4 x 2.

(iv)  Order of A is 4 x 5, order of B is 5 x 1.

The order of the matrix AB is 4 x 1.

(v)  Order of A is 1 x 1, order of B is 1 x 3.

The order of the matrix AB is 1 x 3.

Question 2 :

If A is of order p x q and B is of order q x r what is the order of AB and BA?

Solution :

(p x q) (q x r)  =  p x r

The order of matrix AB is p x r.

(q x r) (p x q)   =  p x r

The product of matrices B and A is not possible.

Hence it is not defined.

Question 3 :

A has ‘a’ rows and ‘a + 3 ’ columns. B has ‘b’ rows and ‘17–b’ columns, and if both products AB and BA exist, find a, b?

Solution :

Number of rows of A = a 

Number of columns of A = a + 3

Number of rows of B = b

Number of columns of A = 17 - b

Since the product of matrices A and B is possible,

[a x (a + 3)] [b x (17 - b)]  

a + 3  =  b

a - b  =  -3  -----(1)

Since the product of matrices B and A is possible,

[b x (17 - b)]  [a x (a + 3)] 

17 - b  =  a

a + b  =  17 ----(2)

(1) + (2)

2a  =  14

a  =  7

By applying the value of a in (1), we get 

7 - b = -3

-b  =  -3 - 7

-b  =  -10

b = 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.