HOW TO FIND THE SLOPE OF A MEDIAN OF A TRIANGLE

Median is a line passing through the midpoint of each side of a triangle.

Let us see how to find the slope of median in a triangle. 

Example :

A triangle has vertices at (6, 7), (2, -9) and (-4, 1). Find the slopes of its medians.

Solution :

Let A(6, 7), B(2, -9) and C(-4, 1) be the vertices of triangle.

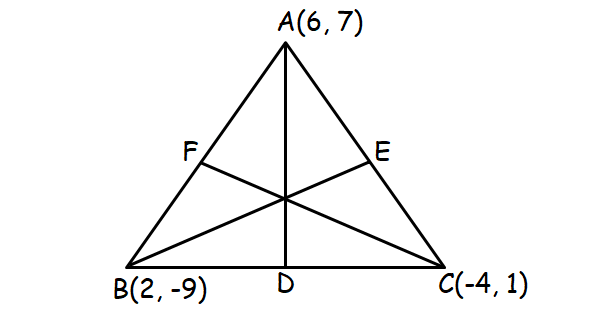
Midpoint of the side BC = D

Midpoint of the side AC = E

Midpoint of the side AB = F

Medians of triangle are AD, BE and CF.

Slope of Median AD :

To find the slope median AD, find the point D which is the midpoint of B and D.

Midpoint formula = ((x₁ + x₂)/2, (y₁ + y₂)/2)

Midpoint of BC = ((2 - 4)/2, (-9 + 1)/2)

= (-2/2, -8/2)

= D(-1, -4)

Using the points A and D, find the slope of the median AD.

A(6, 7), D(-1, -4)

Slope of median AD = (y₂ - y₁)/(x₂ - x₁)

= (-4 - 7)/(-1 - 6)

= -11/(-7)

= 11/7

Slope of Medina BE :

A(6, 7), C(-4, 1)

Midpoint of the side AC = ((6 -4)/2, (7 + 1)/2)

= (2/2, 8/2)

= E(1, 4)

Using the points B and E, find the slope of the median BE.

B(2, -9), E(1, 4)

Slope of median BE = (y₂ - y₁)/(x₂ - x₁)

= (4 + 9)/(1 - 2)

= 13/(-1)

= -13

Slope of Medina CF :

A(6, 7), B(2, -9)

Midpoint of the side AC = (6 + 2)/2, (7 - 9)/2)

= (8/2, -2/2)

= F(4, -1)

Using the points C and F, find the slope of the median CF.

C(-4, 1), F(4, -1)

Slope of median CF = (y₂ - y₁)/(x₂ - x₁)

= (-1 - 4)/(4 - 1)

= -5/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.