HOW TO FIND VERTEX OF A QUADRATIC FUNCTION

The graph of a quadratic function is always a parabola. The vertex of a parabola is the point where the parabola crosses its axis of symmetry.

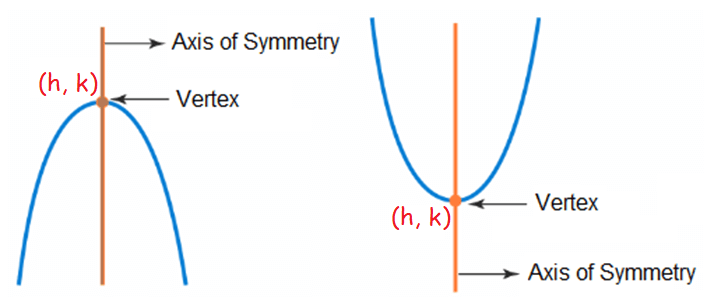
The vertex of a parabola is the highest or lowest point which is also known as maximum or minimum value.

If a parabola opens up, the vertex will be the lowest point and if it opens down, the vertex will be the highest point of the parabola.

Quadratic function in standard form :

f(x) = ax² + bx + c

Quadratic function in in vertex form :

f(x) = a(x - h)² + k

where (h, k) is the vertex.

When a quadratic function is given in vertex form, we can find the vertex easily by taking the values of 'h' and 'k'.

When a quadratic function is given in standard form, you can use formula given below to find the x-coordinate of the vertex.

x = -b/2a

After having found the x-coordinate, you can substitute it into the quadratic function and find the y-coordinate of the vertex.

In each case, find vertex of the quadratic function :

Example 1 :

f(x) = 7x² - 12

Solution :

Comparing f(x) = ax² + bx + c and f(x) = 7x² - 12,

a = 1, b = 0 and c = -12

x-coordinate of the vertex :

x = -b/2a

Substitute a = 7 and b = 0.

x = -0/2(7)

x = 0

y-coordinate of the vertex :

Substitute x = 0 in f(x) = 7x² - 12.

f(0) = 7(0) - 12

= 0 - 12

= -12

y = -12

Vertex of the parabola is (0, -12)

Example 2 :

f(x) = -9x² - 5

Solution :

Comparing f(x) = ax² + bx + c and f(x) = -9x² - 5,

a = -9, b = 0 and c = -5

x-coordinate of the vertex :

x = -b/2a

Substitute a = -9 and b = 0.

x = -0/2(-9)

x = 0

y-coordinate of the vertex :

Substitute x = 0 in f(x) = -9x² - 5.

f(0) = -9(0) - 5

= 0 - 5

= -5

y = -5

Vertex of the parabola is (0, -5)

Example 3 :

f(x) = (x - 2)² - 3

Solution :

The given quadratic function is in standard form.

Comparing f(x) = a(x - h)² + k and f(x) = (x - 2)² - 3,

h = 2 and k = -3

Vertex of the parabola :

(h, k) = (2, -3)

Example 4 :

f(x) = (x + 3)² + 4

Solution :

The given quadratic function is in standard form.

Comparing f(x) = a(x - h)² + k and f(x) = (x + 3)² + 4,

h = -3 and k = 4

Vertex of the parabola :

(h, k) = (-3, 4)

Example 5 :

f(x) = (2x - 5)² + 6

Solution :

Write the given quadratic function in vertex form.

f(x) = (2x - 5)² + 6

f(x) = [2(x - 5/2)]² + 6

f(x) = [2²(x - 5/2)²] + 6

f(x) = 4(x - 5/2)² + 6

Now, the given quadratic function is in standard form.

Comparing f(x) = a(x - h)² + k and f(x) = 4(x - 5/2)² + 6,

h = 5/2 and k = 6

Vertex of the parabola :

(h, k) = (5/2, 6)

Example 6 :

f(x) = (7x + 3)² + 5

Solution :

Write the given quadratic function in vertex form.

f(x) = (7x + 3)² + 5

f(x) = [7(x + 3/7)]² + 5

f(x) = [7²(x + 3/7)²] + 5

f(x) = 49(x + 3/7)² + 5

Comparing f(x) = a(x - h)² + k and f(x) = 49(x + 3/7)² + 5,

h = -3/7 and k = 5

Vertex of the parabola :

(h, k) = (-3/7, 5)

Transform the equation of the parabola to the standard vertex form by completing the square method.

Example 7 :

-x² - 2x + y + 7 = 0

Solution :

Write the given quadratic function in vertex form.

-x² - 2x + y + 7 = 0

y + 7 = [x² + 2x]

y + 7 = [x² + 2x(1) + 1² - 1²]

y + 7 = [(x + 1)² - 1]

y + 7 + 1 = (x + 1)²

y + 8 = (x + 1)²

y = (x + 1)² - 8

Comparing with y = (x - h)² + k

y = (x - (-1))² - 8

So, teh vertex (h, k) is (-1, -8).

Example 8 :

x² - 6x - y + 9 = 0

Solution :

Write the given quadratic function in vertex form.

x² - 6x - y + 9 = 0

x² - 6x = y - 9

x² - 2x(3) + 3² - 3² = y - 9

(x - 3)² - 9 = y - 9

(x - 3)² = y - 9 + 9

(x - 3)² = y

y = (x - 3)²

Comparing with y = (x - h)² + k

y = (x - 3)²

So, the vertex (h, k) is (3, 0).

Example 9 :

-x² + 8x + y + 12 = 0

Solution :

Write the given quadratic function in vertex form.

-x² + 8x + y + 12 = 0

x² - 8x = y + 12

x² - 2x(4) + 4² - 4² = y + 12

(x - 4)² - 16 = y + 12

y + 12 = (x - 4)² - 16

y = (x - 4)² - 16 - 12

y = (x - 4)² - 28

Comparing with y = (x - h)² + k

y = (x - 4)² - 28

So, the vertex (h, k) is (4, -28).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.