HOW TO GRAPH A PARABOLA IN INTERCEPT FORM

Example 1 : 

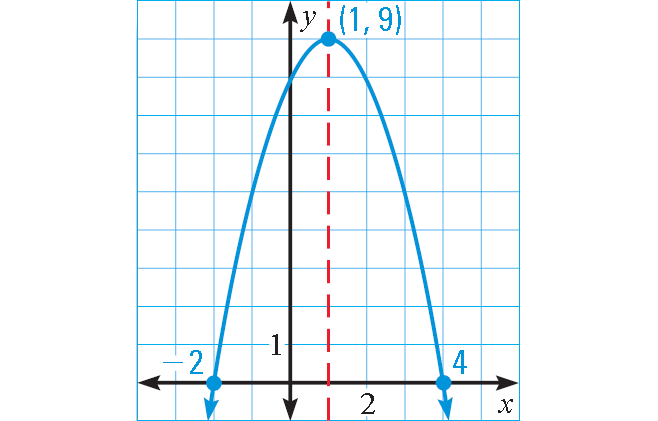
Graph : y = -(x + 2)(x - 4)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = -1, p = -2, and q = 4.

Because a < 0, the parabola opens down.

The x-intercepts occur at (-2, 0) and (4, 0).

The axis of symmetry lies halfway between these points, at x = 1.

So, the x-coordinate of the vertex is x = 1 and the y-coordinate of the vertex is :

y  =  -(1 + 2)(1 - 4)

=  -(3)(-3)

=  9

The graph of the equation is shown below.

Example 2 : 

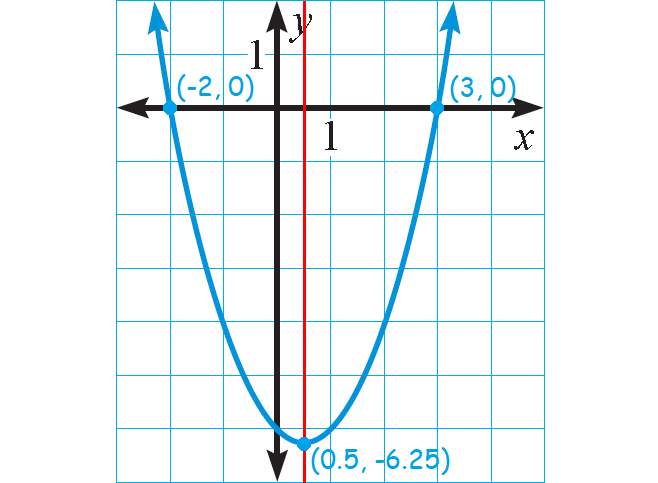
Graph : y = (x + 2)(x - 3)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = 1, p = -2, and q = 3.

Because a > 0, the parabola opens up.

The x-intercepts occur at (-2, 0) and (3, 0).

The axis of symmetry lies halfway between these points, at x = 0.5.

So, the x-coordinate of the vertex is x = 0.5 and the y-coordinate of the vertex is :

y  =  (0.5 + 2)(0.5 - 3)

=  (2.5)(-2.5)

=  -6.25

The graph of the equation is shown below.

Example 3 : 

Graph : y = (x - 4)(x + 2)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = 1, p = 4, and q = -2.

Because a > 0, the parabola opens up.

The x-intercepts occur at (4, 0) and (-2, 0).

Halfway of x-intercepts = 4 + (-2) / 2  ==> 1

The axis of symmetry lies halfway between these points, at x = 1.

So, the x-coordinate of the vertex is x = 1 and the y-coordinate of the vertex is :

y  = (1 - 4)(1 + 2)

=  (-3)(3)

= -9

The graph of the equation is shown below.

y -intercept :

y = (x - 4)(x + 2)

When x = 0

y = (0 - 4) (0 + 2)

y = -8

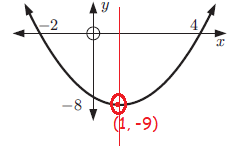
Example 4 : 

Graph : y = -(x - 4)(x + 2)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = -1, p = 4, and q = -2.

Because a < 0, the parabola down.

The x-intercepts occur at (4, 0) and (-2, 0).

Halfway of x-intercepts = 4 + (-2) / 2  ==> 1

The axis of symmetry lies halfway between these points, at x = 1.

So, the x-coordinate of the vertex is x = 1 and the y-coordinate of the vertex is :

y  = -(1 - 4)(1 + 2)

=  -(-3)(3)

= 9

y -intercept :

y = -(x - 4)(x + 2)

When x = 0

y = -(0 - 4) (0 + 2)

y = 8

The graph of the equation is shown below.

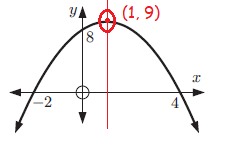
Example 5 : 

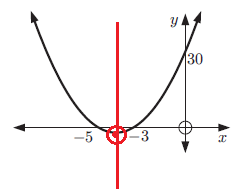
Graph : y = 2(x + 3)(x + 5)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = 2, p = -3, and q = -5.

Because a > 0, the parabola opens up.

The x-intercepts occur at (-3, 0) and (-5, 0).

Halfway of x-intercepts = (-3) + (-5) / 2  ==> -4

The axis of symmetry lies halfway between these points, at x = -4.

So, the x-coordinate of the vertex is x = -4 and the y-coordinate of the vertex is :

y = 2(-4 + 3)(-4 + 5)

= 2(-1)(1)

= -2

y -intercept :

y = 2(x + 3)(x + 5)

When x = 0

y = 2(0 + 3)(0 + 5)

y = 2(3)(5)

y = 30

The graph of the equation is shown below.

Example 6 : 

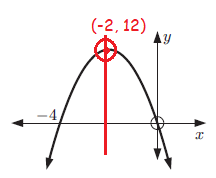
Graph : y = -3x(x + 4)

Solution : 

The equation of the parabola is in intercept form

y  =  a(x - p)(x - q)

where a = -3, p = 0, and q = -4.

Because a < 0, the parabola down.

The x-intercepts occur at (0, 0) and (-4, 0).

Halfway of x-intercepts = 0 + (-4) / 2  ==> -2

The axis of symmetry lies halfway between these points, at x = -2.

So, the x-coordinate of the vertex is x = -2 and the y-coordinate of the vertex is :

y = -3x(x + 4)

y = -3(-2)(-2 + 4)

y = 6(2)

y = 12

Vertex is at (-2, 12)

y -intercept :

y = -3x(x + 4)

When x = 0

y = 3(0)(0+4)

y = 0

The graph of the equation is shown below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.