MULTIPLYING MATRICES
Key Concept
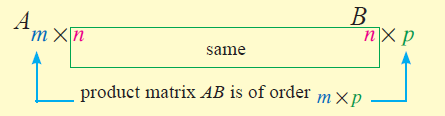
Examples 1-6 : In each case, find the product.
Example 1 :
Solution :
Number of columns of the first matrix = 2
Number of rows of the second matrix = 2
Since the number of columns of the first matrix and number of rows of the second matrix are equal, the above two matrices can be multiplied.
Example 2 :
Solution :
Number of columns of the first matrix = 2
Number of rows of the second matrix = 2
Since the number of columns of the first matrix and number of rows of the second matrix are equal, the above two matrices can be multiplied.
Example 3 :
Solution :
Number of columns of the first matrix = 1
Number of rows of the second matrix = 1
Since the number of columns of the first matrix and number of rows of the second matrix are equal, the above two matrices can be multiplied.
Example 4 :
Solution :
Number of columns of the first matrix = 2
Number of rows of the second matrix = 2
Since the number of columns of the first matrix and number of rows of the second matrix are equal, the above two matrices can be multiplied.
Example 5 :
Solution :
Number of columns of the first matrix = 3
Number of rows of the second matrix = 3
Since the number of columns of the first matrix and number of rows of the second matrix are equal, the above two matrices can be multiplied.
Example 6 :
Solution :
Number of columns of the first matrix = 3
Number of rows of the second matrix = 2
Since the number of columns of the first matrix and number of rows of the second matrix are NOT equal, the above two matrices can NOT be multiplied.
Example 7 :
For the above two matrices A and B, find AXB and BXA and check if AXB = BXA.
Solution :
A X B :
Number of columns of matrix A = 2
Number of rows of matrix B = 2
Since the number of columns of matrix A and number of rows of matrix B are equal, we can find AXB.
B X A :
Number of columns of matrix B = 2
Number of rows of matrix A = 2
Since the number of columns of matrix B and number of rows of matrix A are equal, we can find BXA.
From (1) and (2),
A X B ≠ B X A
From this, we can conclude that matrix multiplication is not commutative.
Example 8 :
Find the value of x :
Solution :
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions
Dec 26, 24 07:41 AM
AP Calculus AB Problems with Solutions -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 23, 24 03:47 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 91)
Dec 23, 24 03:40 AM
Digital SAT Math Problems and Solutions (Part - 91)