INSCRIBED QUADRILATERALS

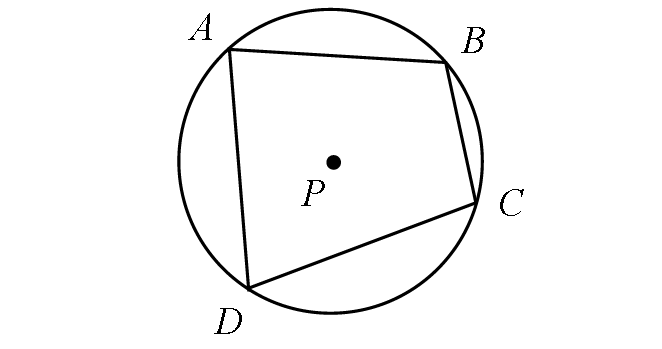
If a quadrilateral inscribed in a circle, then its opposite angles are supplementary.  

In circle P above, 

m∠A + m∠C  =  180°

m∠B + m∠D  =  180°

Solved Examples

Example 1 : 

In the diagram shown below, find the following measures : 

(i) m∠J  and  (ii) m∠K

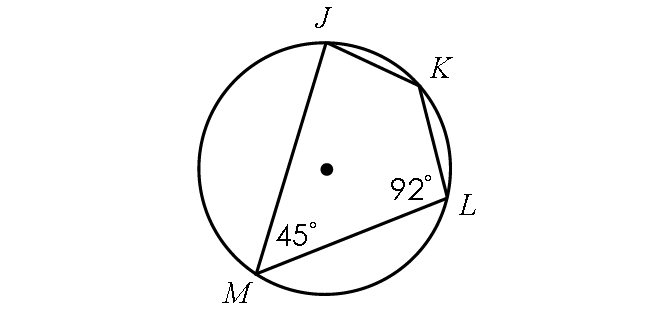
Solution : 

In the above diagram, quadrilateral JKLM is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠J + m∠L  =  180° -----(1)

m∠K + m∠M  =  180° -----(2)

Finding m∠J : 

In (1), substitute m∠L  =  92°. 

m∠J + 92°  =  180°

Subtract 92° from each side. 

m∠J  =  88°

Finding m∠K : 

In (1), substitute m∠M  =  45°. 

m∠K + 45°  =  180°

Subtract 45° from each side. 

m∠J  =  135°

Example 2 : 

In the diagram shown below, find the following measures : 

(i) m∠P, (ii) m∠R  and  (ii) m∠S

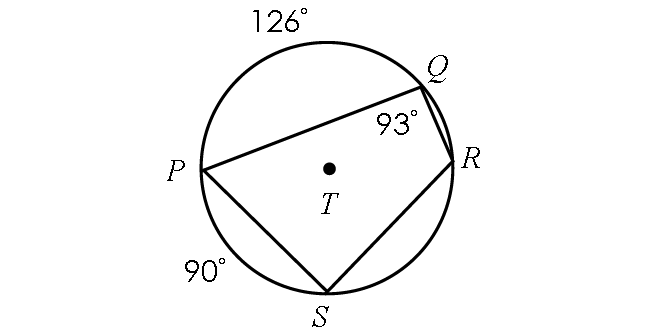
Solution : 

In the above diagram, quadrilateral PQRS is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠P + m∠R  =  180° -----(1)

m∠Q + m∠S  =  180° -----(2)

Finding m∠P : 

In the circle T above,

m∠arc SP + m∠arc PQ + m∠arc QRS  =  360°

90° + 126° + m∠arc QRS  =  360°

216° + m∠arc QRS  =  360°

Subtract 216° from each side. 

m∠arc QRS  =  144°

By Inscribed Angle Theorem, 

m∠P  =  1/2 ⋅ m∠arc QRS

m∠P  =  1/2 ⋅ 144°

m∠P  =  72°

Finding m∠Q : 

In (1), substitute m∠P  =  72°. 

m∠72° + m∠R  =  180°

Subtract 72° from each side. 

m∠R  =  108°

Finding m∠S : 

In (1), substitute m∠Q  =  93°. 

93° + m∠S  =  180°

Subtract 93° from each side. 

m∠S  =  87°

Example 3 : 

In the diagram shown below, find the following measures : 

(i) m∠A, (ii) m∠B, (iii) m∠C  and  (ii) m∠D

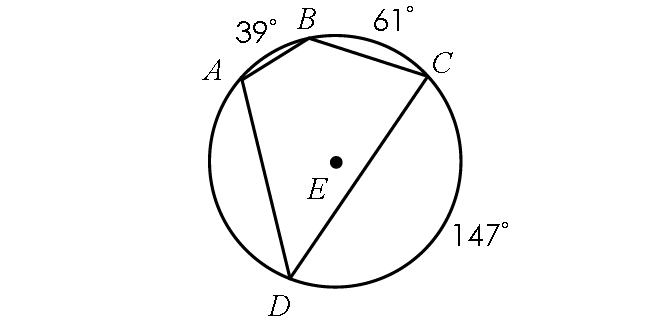
Solution : 

In the above diagram, quadrilateral ABCD is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠A + m∠C  =  180° -----(1)

m∠B + m∠D  =  180° -----(2)

Finding m∠A : 

In the circle T above,

m∠arc BC + m∠arc CD  =  61° + 147°

m∠arc BC + m∠arc CD  =  208°

Then, 

m∠arc BCD  =  208°

By Inscribed Angle Theorem, 

m∠A  =  1/2 ⋅ m∠arc BCD

m∠A  =  1/2 ⋅ 208°

m∠A  =  104°

Finding m∠C : 

In (1), substitute m∠A  =  104°. 

m∠104° + m∠C  =  180°

Subtract 104° from each side. 

m∠C  =  76°

Finding m∠D : 

In the circle T above,

m∠arc AB + m∠arc BC  =  39° + 61°

m∠arc AB + m∠arc BC  =  100°

Then, 

m∠arc ABC  =  100°

By Inscribed Angle Theorem, 

m∠D  =  1/2 ⋅ m∠arc ABC

m∠D  =  1/2 ⋅ 100°

m∠D  =  50°

Finding m∠B : 

In (2), substitute m∠D  =  50°. 

m∠B + 50°  =  180°

Subtract 50° from each side. 

m∠B  =  130°

Example 4 : 

Solve for x. 

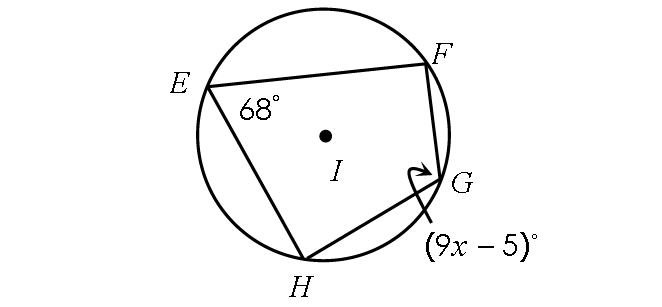
Solution : 

In the above diagram, quadrilateral EFGH is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠E + m∠G  =  180°

68° + (9x - 5)°  =  180°

68 + 9x - 5  =  180

9x + 63  =  180°

Subtract 63 from each side. 

9x  =  117

Divide each side by 9.

x  =  13

Example 5 : 

Solve for x. 

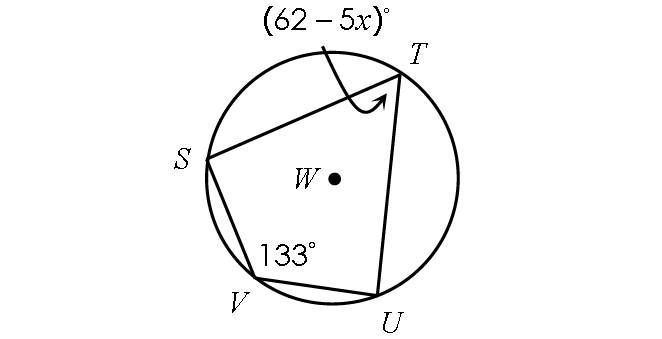
Solution : 

In the above diagram, quadrilateral EFGH is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠E + m∠G  =  180°

68° + (9x - 5)°  =  180°

68 + 9x - 5  =  180

9x + 63  =  180°

Subtract 63 from each side. 

9x  =  117

Example 6 : 

Solve for x. 

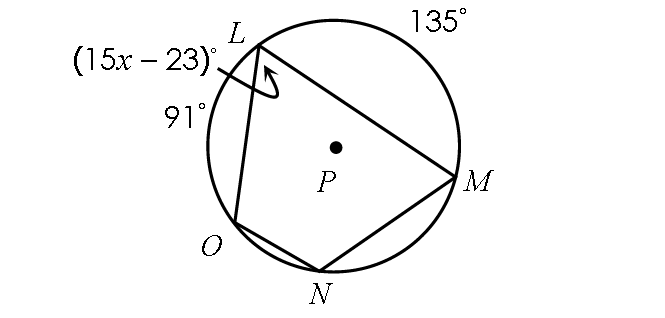
Solution : 

In the above diagram, quadrilateral LMNO is inscribed in a circle. Then, its opposite angles are supplementary.  

m∠L + m∠N  =  180° -----(1)

In the circle P above, 

m∠arc OL + m∠arc LM  =  91° + 135°

m∠arc OL + m∠arc LM  =  226°

Then, 

m∠arc OLM  =  226°

By Inscribed Angle Theorem, 

m∠N  =  1/2 ⋅ m∠arc OLM

m∠N  =  1/2 ⋅ 226°

m∠N  =  113°

In (1), substitute m∠L  =  (15x - 23)° and m∠N  =  113°.

(15x - 23)° + 113°  =  180°

15x - 23 + 113  =  180

15x + 90  =  180

Subtract 90 from each side. 

15x  =  90

Divide each side by 15.

x  =  6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.