INTERIOR ANGLES OF A POLYGON WORKSHEET

Problems 1-4 : Find the measure of each interior angle in the regular polygon given.

Problem 1 :

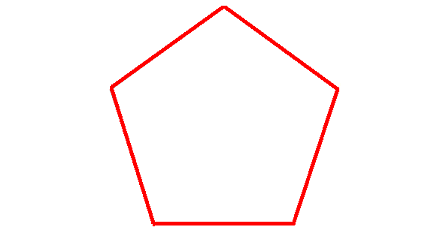
Problem 2 :

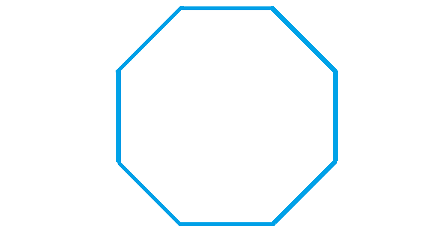
Problem 3 :

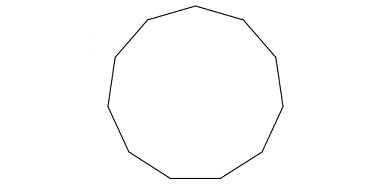
Problem 4 :

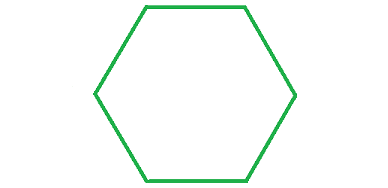
Problem 5 :

What is the value of a in the polygon shown below?

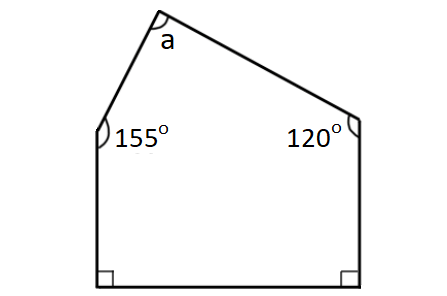
Problem 6 :

Find the value of k in the polygon shown below.

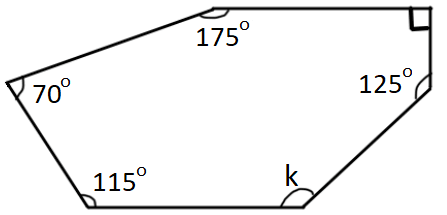
Problem 7 :

Find the value of y in the polygon shown below.

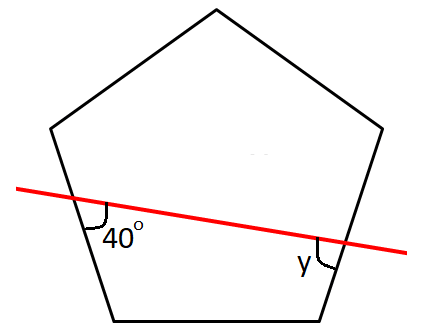
Problem 8 :

What is the measure of each interior angle of a regular heptagon?

Problem 9 :

Sum of the interior angles of a polygon is 1800°. Find the number of sides the polygon has.

Problem 10 :

In a dodecagon, if the measure of each interior angle is 3x°, What is the value of x?

Problem 11 :

The average of all interior angles of a polygon is 156°. Find the number of sides the polygon has.

Problem 12 :

In a regular nonagon, the measure of each interior angle is (3x - 40)°. What is the value of x?

Answers

1. Answer :

Count the number of sides in the given regular polygon.

The given regular polygon has 5 sides.

Formula to find the sum of interior angles of a polygon :

= (n - 2) x 180°

Substitute n = 5.

= (5 - 2) x 180°

= 3 x 180°

= 540°

Measure of each interior angle :

= 540°/5

= 108°

2. Answer :

Count the number of sides in the given regular polygon.

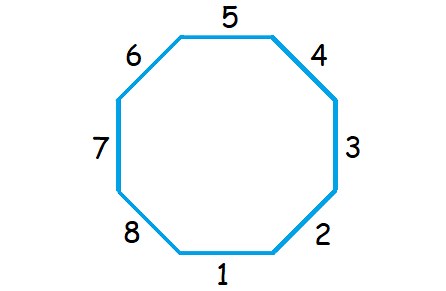
The given regular polygon has 8 sides.

Formula to find the sum of interior angles of a polygon :

= (n - 2) x 180°

Substitute n = 8.

= (8 - 2) x 180°

= 6 x 180°

 = 1080°

Measure of each interior angle :

= 1080°/8

= 135°

3. Answer :

Count the number of sides in the given regular polygon.

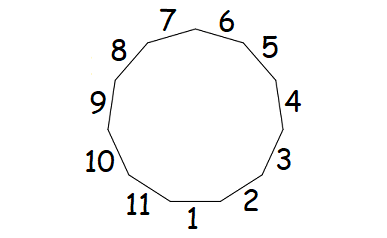
The given regular polygon has 8 sides.

Formula to find the sum of interior angles of a polygon :

= (n - 2) x 180°

Substitute n = 11.

= (11 - 2) x 180°

= 9 x 180°

 = 1620°

Measure of each interior angle :

= 1620°/11

= 147° 3'

4. Answer :

Count the number of sides in the given regular polygon.

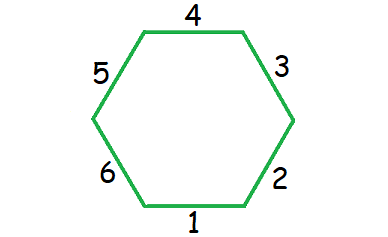
The given regular polygon has 8 sides.

Formula to find the sum of interior angles of a polygon :

= (n - 2) x 180°

Substitute n = 6.

= (6 - 2) x 180°

= 4 x 180°

 = 720°

Measure of each interior angle :

= 720°/6

= 120°

5. Answer :

The given polygon has 5 sides.

Sum of interior angles of the polygon = (5 - 2) x 180°

a + 120° + 90° + 90° + 155° = 3 x 180°

a + 455° = 540°

Subtract 455° from both sides.

x = 85°

6. Answer :

The given polygon has 6 sides.

Sum of interior angles of the polygon = (6 - 2) x 180°

k + 125° + 90° + 175° + 70° + 115° = 4 x 180°

k + 575° = 720°

Subtract 575° from both sides.

k = 145°

7. Answer :

Sum of the interior angles of a regular pentagon :

= (5 - 2) x 180°

= 3 x 180°

= 540°

Measure of each interior angle of a regular polygon :

= 540°/5

= 108°

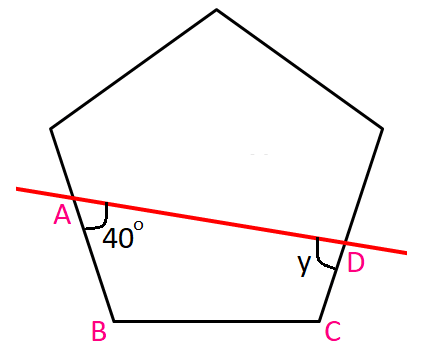
In a regular pentagon, all the interior angles are equal in measure.

m∠C = m∠D = 108°

In the figure above, ABCD is a quadrilateral.

Sum of the interior angles in a quadrilateral = 360°

m∠A + m∠B + m∠C + m∠D = 360°

40° + x + 108° + 108° = 360°

x + 256° = 308°

Subtract 256° from both sides.

x = 52°

8. Answer :

What is the measure of each interior angle of a regular heptagon?

Sum of interior angles of a heptagon :

= (7 - 2) x 180°

= 5 x 180°

= 900°

Measure of each interior angle of a regular hexagon :

= 900°/7

≈ 128.57°

9. Answer :

Sum of the interior angles of a polygon is 1800°. Find the number of sides the polygon has.

Sum of interior angles of the polygon = 1800°

(n - 2) x 180° = 1800°

Divide both sides by 180°.

n - 2 = 10

Add 2 to both sides.

n = 12

Therefore, the polygon has 12 sides.

10. Answer :

Decagon is a 12-sided polygon.

Sum of interior angles of a dodecagon : (12 - 2) x 180°

= 10 x 180°

= 1800°

Since dodecagon is a 12-sided polygon, it will have twelve interior angles

Given : The measure each interior angle of a regular dodecagon is 3x°.

12 x measure of each interior angle = 1800°

12(3x°) = 1800°

36x = 1800

Divide both sides by 36.

x = 50

11. Answer :

Let n be the number of sides the polygon has.

Given : The average of all interior angles of a polygon is 156°.

(Sum of all interior angles of the polygon)/n = 156°

Sum of interior angles of the polygon = n x 156°

(n - 2) x 180° = n x 156°

n x 180° - 2 x 180° = n x 156°

180n - 360 = 156n

Subtract 156n from both sides.

24n - 360 = 0

Add 360 to both sides.

24n = 360

Divide both sides by 24.

n = 15

Therefore, the polygon has 15 sides.

12. Answer :

Dodecagon is a 9-dided polygon

Sum of interior angles of a nonagon : 

= (9 - 2) x 180°

= 7 x 180°

= 1260°

Measure of each interior angle of a regular nonagon :

= 1260°/9

= 140°

Given : The measure of each interior angle of a regular nonagon is (3x - 40)°.

(3x - 40)° = 140°

3x - 40 = 140

Add 40 to both sides.

3x = 180

Divide both sides by 3.

x = 60

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.